题目内容
(13分)已知函数f(x)=ax+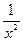 (x≠0,常数a∈R).
(x≠0,常数a∈R).
(1)讨论函数f(x)的奇偶性,并说明理由;
(2)若函数f(x)在x∈[3,+∞)上为增函数,求a的取值范围.
解:(1)定义域(-∞,0)∪(0,+∞),关于原点对称.
当a=0时,f(x)=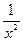 ,满足对定义域上任意x,f(-x)=f(x),
,满足对定义域上任意x,f(-x)=f(x),
∴a=0时,f(x)是偶函数;
当a≠0时,f(1)=a+1,f(-1)=1-a,
若f(x)为偶函数,则a+1=1-a,a=0矛盾;
若f(x)为奇函数,则1-a=-(a+1),1=-1矛盾,∴当a≠0时,f(x)是非奇非偶函数.
(2)任取x1>x2≥3,f(x1)-f(x2)=ax1+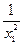 -ax2-
-ax2-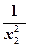
=a(x1-x2)+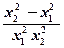 =(x1-x2)(a-
=(x1-x2)(a-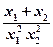 ).
).
∵x1-x2>0,f(x)在[3,+∞)上为增函数,
∴a>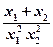 ,即a>
,即a>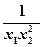 +
+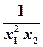 在[3,+∞)上恒成立.
在[3,+∞)上恒成立.
∵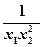 +
+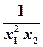 <
<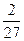 ,∴a≥
,∴a≥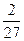 .
.
解析

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
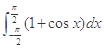 等于( )
等于( )
A.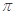 | B.2 | C.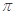 -2 -2 | D.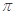 +2 +2 |
 ) .已知函数y=
) .已知函数y=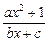 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<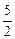
 精确到1万元)。
精确到1万元)。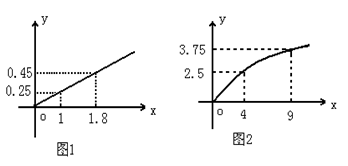
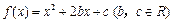 ,且
,且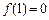 .
.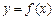 与x轴的两个交点
与x轴的两个交点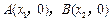 之间的距离为2,求b的值;
之间的距离为2,求b的值; 的两个实数根分别在区间
的两个实数根分别在区间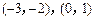 内,求b的取值范围.
内,求b的取值范围.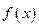 在定义域
在定义域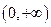 上为增函数,且满足
上为增函数,且满足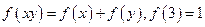
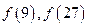 的值 (2)解不等式
的值 (2)解不等式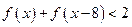
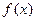 有最小正周期4,且
有最小正周期4,且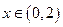 时,
时,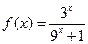 。
。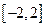 上的解析式;
上的解析式;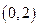 上的单调性,并给予证明;
上的单调性,并给予证明;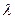 为何值时,关于方程
为何值时,关于方程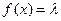 在
在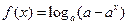
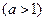 ,求
,求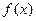 的定义域和值域;
的定义域和值域; 的图象如图所示,则导函数
的图象如图所示,则导函数 的图象的大致形状是( )
的图象的大致形状是( ) 
