题目内容
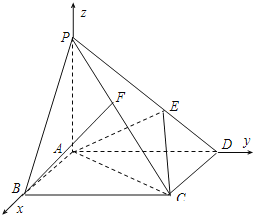
【题目】在底面是正方形的四棱锥![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(Ⅰ)易证![]() ,
, ![]() ,从而可证
,从而可证![]() 平面
平面![]() ;
;
(Ⅱ)以A为坐标原点,直线![]() 分别x轴、y轴、z轴,建立空间直角坐标系,求得平面ACE的法向量为
分别x轴、y轴、z轴,建立空间直角坐标系,求得平面ACE的法向量为![]() ,及平面ACD的法向量
,及平面ACD的法向量![]() ,由法向量夹角公式求解即可.
,由法向量夹角公式求解即可.
试题解析:
(1)正方形ABCD边长为1,PA=1, ![]() ,
,
所以![]() ,即
,即![]() ,
,
根据直线和平面垂直的判定定理,有![]() 平面
平面![]() .
.
(2)如图,以A为坐标原点,直线![]() 分别x轴、y轴、z轴,建立空间直角坐标系.
分别x轴、y轴、z轴,建立空间直角坐标系.
则![]() ,
,
由(1)知![]() 为平面ACD的法向量,
为平面ACD的法向量, ![]() ,
,
设平面ACE的法向量为![]() ,
,
则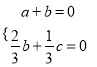
令![]() ,则
,则![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则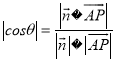 =
=![]() ,
,
又有图可知, ![]() 为锐角,
为锐角,
故所求二面角的余弦值为![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
【题目】已知函数f(x)的定义域为[﹣1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.
x | ﹣1 | 0 | 4 | 5 |
f(x) | 1 | 2 | 2 | 1 |
下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[﹣1,t]时,f(x)的最大值是2,那么t的最大值为5;
④当1<a<2时,函数y=f(x)﹣a有4个零点.
其中所有真命题的序号为 . 



