题目内容
从一个半径为1的圆形铁片中剪出圆心角为x弧度的一个扇形,并将其卷成一个圆锥(不考虑连接用料),若圆锥的容积达到最大时,则x的值是________.

分析:设圆锥的底面半径为r,高为h,体积为V,求出r2+h2=R2,表示出体积表达式,利用导数求出函数的最大值,得到结果.
解答:
 解:设圆锥的底面半径为r,高为h,体积为V,那么r2+h2=R2,
解:设圆锥的底面半径为r,高为h,体积为V,那么r2+h2=R2,因此,V=
 πr2h
πr2h=
 π(R2-h2)h=
π(R2-h2)h= πR2h-
πR2h- πh3(0<h<R).…(3分)
πh3(0<h<R).…(3分)V′=
 πR2-πh2.
πR2-πh2.令V'=0,即
 πR2-πh2=0,得 h=
πR2-πh2=0,得 h= R.…(5分)
R.…(5分)当 0<h<
 R时,V'>0.
R时,V'>0.当
 R<h<R时,V'<0.
R<h<R时,V'<0.所以,h=
 R时,V取得极大值,并且这个极大值是最大值.…(8分)
R时,V取得极大值,并且这个极大值是最大值.…(8分) 把 h=
 R代入r2+h2=R2,得 r=
R代入r2+h2=R2,得 r= R.
R.由Rx=2πr,得 x=
 π.
π.故答案为:
 .
.点评:本题考查圆锥与扇形展开图的关系,体积的计算,考查计算能力,导数的应用,解题的关键是建立起体积的函数模型,理解函数的单调性与最值的关系是解本题的重点.

练习册系列答案
相关题目
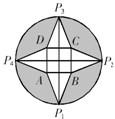 如图,从一个半径为(1+
如图,从一个半径为(1+| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
