题目内容
已知向量
(1)求 ;
;
(2)若 的值域.
的值域.
解:(1) =cos
=cos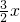 cos
cos +sin
+sin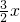 sin
sin =cosx
=cosx
 =
= =2+2cosx,
=2+2cosx,
∵x∈ ,
,
∴ |=2cos
|=2cos ;
;
(2) =cosx-2cos
=cosx-2cos =2cos2
=2cos2 -2cos
-2cos -1
-1
令t=cos,则f(t)=2t2-2t-1=2(t- )2-
)2-
∵x∈ ,
,
∴
∴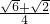 ≤t≤
≤t≤ ,
,
∴函数在( ,+∞)上单调增
,+∞)上单调增
∴f(t)∈[ ,
, ]
]
分析:(1)利用数量积公式及差角的余弦公式可求 ,将模先平方再开方,可得结论;
,将模先平方再开方,可得结论;
(2)利用换元法,再利用配方法,即可求函数的值域.
点评:本题考查数量积公式,考查三角函数的化简,考查函数的值域,解题的关键是正确化简三角函数.
 =cos
=cos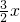 cos
cos +sin
+sin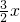 sin
sin =cosx
=cosx =
= =2+2cosx,
=2+2cosx,∵x∈
 ,
,∴
 |=2cos
|=2cos ;
;(2)
 =cosx-2cos
=cosx-2cos =2cos2
=2cos2 -2cos
-2cos -1
-1令t=cos,则f(t)=2t2-2t-1=2(t-
 )2-
)2-
∵x∈
 ,
,∴

∴
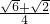 ≤t≤
≤t≤ ,
,∴函数在(
 ,+∞)上单调增
,+∞)上单调增∴f(t)∈[
 ,
, ]
]分析:(1)利用数量积公式及差角的余弦公式可求
 ,将模先平方再开方,可得结论;
,将模先平方再开方,可得结论;(2)利用换元法,再利用配方法,即可求函数的值域.
点评:本题考查数量积公式,考查三角函数的化简,考查函数的值域,解题的关键是正确化简三角函数.

练习册系列答案
相关题目
 .
. ;
; 与
与 平行,求
平行,求 的值;
的值;
 ,并求
,并求 在
在 上的投影
上的投影 ,求
,求 的值,并确定此时它们是同向还是反向?
的值,并确定此时它们是同向还是反向?
 的坐标表示;
的坐标表示; 的值
的值