题目内容
7.已知A(4,-3)、B(2,-1)和直线1:4x+y-2=0,在直线l上求一点P使|PA|=|PB|.分析 在直线l上求一点P使|PA|=|PB|,即所求的点是线段AB的中垂线与已知直线的交点.
解答 解:在直线l上求一点P使|PA|=|PB|,即所求的点是线段AB的中垂线与已知直线的交点为P.
A(4,-3)、B(2,-1)两点的中点为D(3,-2),
线段AB的斜率${k}_{1}=\frac{-1+3}{2-4}$=-1,
∴线段AB中垂线的斜率k2=1,
∴中垂线的方程为y+2=(x-3)
线段AB中垂线与已知直线联立方程得到:
$\left\{\begin{array}{l}{y+2=x-3}\\{4x+y-2=0}\end{array}\right.$,解得x=$\frac{7}{5}$,y=-$\frac{18}{5}$,
所以得到P($\frac{7}{5}$,-$\frac{18}{5}$).
点评 本题考查使得线段相等的点的坐标的求法,是中档题,解题时要注意中点坐标公式、直线垂直的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
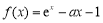 (
(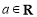 ).
).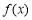 的单调区间;
的单调区间;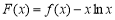 在定义域内存在零点,求
在定义域内存在零点,求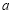 的取值范围.
的取值范围.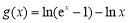 ,当
,当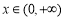 时,不等式
时,不等式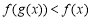 恒成立,求
恒成立,求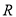 上的奇函数
上的奇函数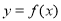 ,对于
,对于 都有
都有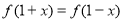 ,当
,当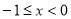 时,
时,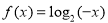 ,则函数
,则函数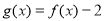 在
在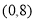 内所有的零点之和为( )
内所有的零点之和为( )