题目内容
若n∈N*，n＜100，且二项式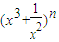
的展开式中存在常数项，则所有满足条件的n值的和是 ．
【答案】分析：写出二项式
的展开式的通项，令x的指数为0，可得n是5的倍数，结合n＜100，即可求得所有满足条件的n值的和．
解答：解：二项式
的展开式的通项为
=
令3n-5r=0，可得3n=5r
∴n是5的倍数
∵n＜100
∴所有满足条件的n值的和=5+10+…+95=950
故答案为：950
点评：本题考查二项式定理的运用，考查展开式中的特殊性，确定展开式的通项是关键．
的展开式的通项，令x的指数为0，可得n是5的倍数，结合n＜100，即可求得所有满足条件的n值的和．解答：解：二项式
的展开式的通项为=令3n-5r=0，可得3n=5r
∴n是5的倍数
∵n＜100
∴所有满足条件的n值的和=5+10+…+95=950
故答案为：950
点评：本题考查二项式定理的运用，考查展开式中的特殊性，确定展开式的通项是关键．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
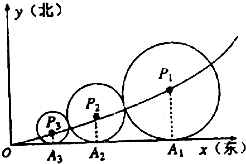为建设好长、株、潭“两型社会”改革实验区，加快二市经济一体化进程，某规划部门在三市的交界处拟建一个大型环保生态公园，并在公园入口处的东南方位建造一个供市民休闲健身的小型绿化广场，如图是步行小道设计方案示意图，其中，Ox，Oy分别表示自西向东，自南向北的两条主干道，设计方案是自主干道交汇点O处修一条步行小道，小道为抛物线y=x2的一段，在小道上依次以点