题目内容
在△ABC中,下列结论正确的个数是________.
①A>B?cosA<cosB;②A>B?sinA>sinB;③A>B?cos2A<cos2B.
3个
分析:由函数 y=cosx 在(0,π)上是减函数,可得 A>B?cosA<cosB,故①正确;由A>B?a>b及正弦定理可得②正确;
由A>B?sinA>sinB>0 以及二倍角公式,可得③正确.
解答:在△ABC中,由于 0<A、B<π,由函数 y=cosx 在(0,π)上是减函数,可得 A>B?cosA<cosB,故①正确.
在△ABC中,由于A>B?a>b,由正弦理可得 a=2rsinA,b=2rsinB,∴A>B?sinA>sinB,故②正确.
在△ABC中,由以上可得A>B?sinA>sinB>0?1-2sin2A<1-2sin2B?cos2A<cos2B,故③正确.
故答案为 3个.
点评:本题主要考查正弦函数的单调性、余弦函数的单调性,正弦定理、及二倍角公式的应用,属于中档题.
分析:由函数 y=cosx 在(0,π)上是减函数,可得 A>B?cosA<cosB,故①正确;由A>B?a>b及正弦定理可得②正确;
由A>B?sinA>sinB>0 以及二倍角公式,可得③正确.
解答:在△ABC中,由于 0<A、B<π,由函数 y=cosx 在(0,π)上是减函数,可得 A>B?cosA<cosB,故①正确.
在△ABC中,由于A>B?a>b,由正弦理可得 a=2rsinA,b=2rsinB,∴A>B?sinA>sinB,故②正确.
在△ABC中,由以上可得A>B?sinA>sinB>0?1-2sin2A<1-2sin2B?cos2A<cos2B,故③正确.
故答案为 3个.
点评:本题主要考查正弦函数的单调性、余弦函数的单调性,正弦定理、及二倍角公式的应用,属于中档题.

练习册系列答案
相关题目
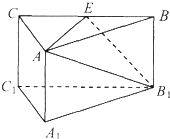 如图,在正三棱柱A1B1C1-ABC中,E是BC中点,则下列结论正确的是( )
如图,在正三棱柱A1B1C1-ABC中,E是BC中点,则下列结论正确的是( ) (2013•普陀区二模)如图,△ABC是边长为1的正三角形,点P在△ABC所在的平面内,且
(2013•普陀区二模)如图,△ABC是边长为1的正三角形,点P在△ABC所在的平面内,且