题目内容
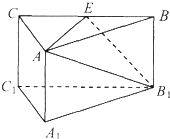 如图,在正三棱柱A1B1C1-ABC中,E是BC中点,则下列结论正确的是( )
如图,在正三棱柱A1B1C1-ABC中,E是BC中点,则下列结论正确的是( )分析:根据空间直线的位置关系,可得CC1与B1E是相交直线,A1C1∥平面AB1E不成立,故A、C项不正确;根据线面垂直的定义与性质,可得AC⊥平面ABB1A1不成立,得C项不正确;最后根据异面直线的定义与面面垂直的判定,得到D项的两个结论都正确.由此可得正确答案.
解答:解:对于A,因为CC1与B1E同在平面BB1C1C中,所以CC1与B1E不是异面直线,
因此A项不正确;
对于B,若AC⊥平面ABB1A1,则AC⊥AB,得∠CAB=90°
这与正△ABC中∠CAB=60°矛盾,因此B项不正确;
对于C,因为直线AC与平面AB1E相交,而A1C1∥AC,
所以A1C1∥平面AB1E不成立,故C项不正确;
对于D,直线AE与B1C1既不相交也不平行,故AE、B1C1是异面直线
又∵直线AE⊥BC,平面ABC⊥平面BB1C1C,平面ABC∩平面BB1C1C=BC
∴AE⊥平面BB1C1C,可得AE⊥B1C1
由此可得D项结论正确
故选:D
因此A项不正确;
对于B,若AC⊥平面ABB1A1,则AC⊥AB,得∠CAB=90°
这与正△ABC中∠CAB=60°矛盾,因此B项不正确;
对于C,因为直线AC与平面AB1E相交,而A1C1∥AC,
所以A1C1∥平面AB1E不成立,故C项不正确;
对于D,直线AE与B1C1既不相交也不平行,故AE、B1C1是异面直线
又∵直线AE⊥BC,平面ABC⊥平面BB1C1C,平面ABC∩平面BB1C1C=BC
∴AE⊥平面BB1C1C,可得AE⊥B1C1
由此可得D项结论正确
故选:D
点评:本题在正三棱柱中判定线面平行、线面垂直,并判断两条直线是否异面.着重考查了空间直线与直线位置、直线与平面平行垂直的判定等知识,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB=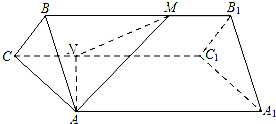 (2013•徐州三模)如图,在正三棱柱ABC-A1B1C1中,已知AA1=6,AB=2,M,N分别是棱BB1,CC1上的点,且BM=4,CN=2.
(2013•徐州三模)如图,在正三棱柱ABC-A1B1C1中,已知AA1=6,AB=2,M,N分别是棱BB1,CC1上的点,且BM=4,CN=2. 如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=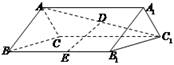
 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.