题目内容
若函数f(x)和g(x)的定义域、值域都是R，则不等式f(x)> g(x)有解的充要条件是（ ）
| A．$ x∈R, f(x)>g(x) | B．有无穷多个x (x∈R )，使得f(x)>g(x) |
| C．" x∈R,f(x)>g(x) | D．{ x∈R| f(x)≤g(x)}=F |
A
解析试题分析：若不等式f(x)> g(x)有解，则$ x∈R, f(x)>g(x)；若$ x∈R, f(x)>g(x)，则不等式f(x)> g(x)有解，所以不等式f(x)> g(x)有解的充要条件是$ x∈R, f(x)>g(x)。故选Ａ。
考点：充分条件与必要条件
点评：本题用到结论：若
，则
互为充要条件。
练习册系列答案
ABC考王全优卷系列答案
相关题目
给出下面四个命题：
（1）如果直线
，那么
可以确定一个平面；（2）如果直线
和
都与直线
相交，那么可以确定一个平面；（3）如果
那么可以确定一个平面；（4）直线过平面
内一点与平面外一点，直线在平面内不经过该点，那么和是异面直线。上述命题中，真命题的个数是（ ）
| A．1个； | B．2个； | C．3个； | D．4个。 |
下列说法中，错误的是 （ ）
A． |
B．若 的逆否命题为真命题 |
C．命题 |
D．若 |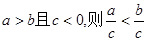
“
”是“
”的( )
| A．充分非必要条件 | B．充分必要条件 | C．必要非充分条件 | D．非充分必要条件 |
设
是空间两条直线，
是空间一个平面．当
时，“
”是“
”的
| A．充要条件 | B．充分不必要条件 |
| C．必要不充分条件 | D．既不充分也不必要条件 |
下列判断正确的是( )
A．“ ”是“ ”的充要条件 |
B．命题“ ”的否定是“ ” |
C．若 均为假命题，则 为真命题 |
| D．一个命题连同它的逆命题、否命题、逆否命题，这四个命题中不可能恰有一个真命题 |
已知a，b，c∈R，命题“若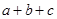
=3，则
≥3”的否命题是（ ）
| A．若a+b+c≠3，则<3 | B．若a+b+c=3，则<3 |
| C．若a+b+c≠3，则≥3 | D．若≥3，则a+b+c=3 |
设
R，则“
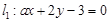”是“直线
与直线
平行”的( )条件
| A．充分不必要 | B．必要不充分 |
| C．充要 | D．既不充分也不必要 |
给定两个命题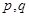
，
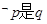的必要而不充分条件，则
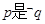的( )
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |