题目内容
设![]() 是虚数
是虚数![]() 是实数,且
是实数,且![]() .
.
(1)求![]() 的值及
的值及![]() 的实部的取值范围.
的实部的取值范围.
(2)设![]() ,求证:
,求证:![]() 为纯虚数;
为纯虚数;
(3)求![]() 的最小值.
的最小值.
(1)![]() ,
, ![]() 的实部的取值范围是
的实部的取值范围是![]() ;
;
(2)证明见解析(3)![]() 时,
时,![]() 取得最小值1.
取得最小值1.
解析:
(1)解:设![]() ,
,
则![]()
![]() .
.
因为![]() 是实数,
是实数,![]() ,所以
,所以![]() ,即
,即![]() .
.
于是![]() ,即
,即![]() ,
,![]() .
.
所以![]() 的实部的取值范围是
的实部的取值范围是![]() ;
;
(2)证明:![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() 为纯虚数;
为纯虚数;
(3)解:![]()
![]()
![]()
因为![]() ,所以
,所以![]() ,
,
故![]()
![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 取得最小值1.
取得最小值1.

练习册系列答案
相关题目
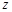 是虚数
是虚数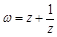 是实数,且
是实数,且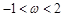 .
.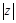 的值及
的值及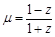 ,求证:
,求证: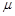 为纯虚数;
为纯虚数;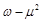 的最小值.
的最小值.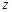 是虚数
是虚数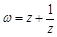 是实数,且
是实数,且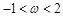 .
.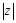 的值及
的值及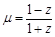 ,求证:
,求证: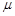 为纯虚数;
为纯虚数;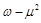 的最小值.
的最小值.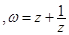 是实数,且
是实数,且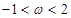 .
. 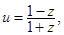 求证:u为纯虚数;
求证:u为纯虚数; 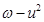 的最小值.
的最小值.