题目内容
设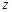 是虚数
是虚数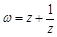 是实数,且
是实数,且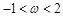 .
.
(1)求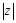 的值及
的值及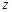 的实部的取值范围.
的实部的取值范围.
(2)设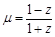 ,求证:
,求证: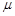 为纯虚数;
为纯虚数;
(3)求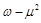 的最小值.
的最小值.
【答案】
(1)见解析;(2) 时,
时, 取得最小值1.
取得最小值1.
【解析】
试题分析:
(1)解:设 ,
,
则
 .
.
因为 是实数,
是实数, ,所以
,所以 ,即
,即 .
.
于是 ,即
,即 ,
, .
.
所以 的实部的取值范围是
的实部的取值范围是 ;
;
(2)证明: .
.
因为 ,
, ,所以
,所以 为纯虚数;
为纯虚数;
(3)解:


因为 ,所以
,所以 ,
,
故
 .
.
当 ,即
,即 时,
时, 取得最小值1.
取得最小值1.
考点:本题主要考查复数的概念及代数运算,均值定理的应用。
点评:综合题,对学生运用数学知识分析问题解决问题的能力要求较高。解答(2)题关键点有两个,一是能否构建函数模型,二是如何求函数的最值。

练习册系列答案
相关题目
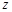 是虚数
是虚数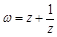 是实数,且
是实数,且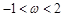 .
.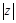 的值及
的值及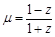 ,求证:
,求证: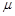 为纯虚数;
为纯虚数;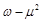 的最小值.
的最小值.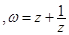 是实数,且
是实数,且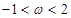 .
. 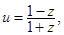 求证:u为纯虚数;
求证:u为纯虚数; 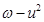 的最小值.
的最小值.