题目内容
((本小题满分14分)
已知函数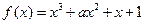 ,(
,(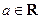 )
)
(Ⅰ)讨论函数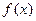 的单调区间;
的单调区间;
(Ⅱ)设函数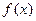 在区间
在区间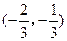 内是减函数,求
内是减函数,求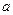 的取值范围.
的取值范围.
已知函数
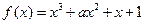 ,(
,(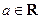 )
)(Ⅰ)讨论函数
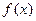 的单调区间;
的单调区间;(Ⅱ)设函数
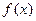 在区间
在区间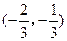 内是减函数,求
内是减函数,求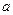 的取值范围.
的取值范围.解:(1)

 …………………………………………………………………1分
…………………………………………………………………1分当
 时,即
时,即 时,
时, ,
,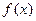 在
在 上递增;…………………………………………………3分
上递增;…………………………………………………3分当
 时,即
时,即 或
或 时,
时, ,
,由
 求得两根为
求得两根为 …………………………………5分
…………………………………5分即
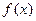 在
在 和
和 上递增;
上递增;在
 上递减,………………………………6分
上递减,………………………………6分
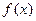 的单调递增区间是:当
的单调递增区间是:当 时,
时,
当
 或
或 时,
时, 和
和
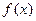 的单调递减区间是:
的单调递减区间是:当
 或
或 时,
时, ………………7分
………………7分(2)(法一)由(1)知
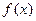 在区间
在区间 上递减,
上递减,∴只要


∴
 解得:
解得: .
. ………9分
………9分 ……………………………………………………………12分
……………………………………………………………12分
 ……………………………………………………14分
……………………………………………………14分略

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
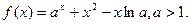
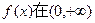 上单调递增;
上单调递增;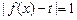 有三个不同的实根,求t的值;
有三个不同的实根,求t的值; 的取值范围。
的取值范围。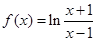
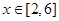
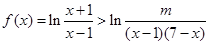 恒成立,求实数
恒成立,求实数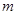 的取值范围;
的取值范围;
 在点
在点 处的切线方程。
处的切线方程。 在区间
在区间 内单调递增,求
内单调递增,求 的取值范围。
的取值范围。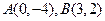 ,抛物线
,抛物线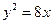 上的点到直线
上的点到直线 的最短距离___ 。
的最短距离___ 。 是减函数的区间为( )
是减函数的区间为( ) B.(0,4) C.
B.(0,4) C. D
D .
.
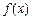 为可导函数,
为可导函数,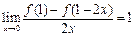 ,则在点(1,
,则在点(1,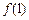 )处的切线斜率为
)处的切线斜率为
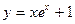 在点(0,1)处的切线方程是 ( )
在点(0,1)处的切线方程是 ( )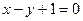
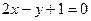
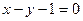
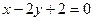
 ,
, ,…,
,…, ,n=1,2,3,….满足
,n=1,2,3,….满足 的点x∈[0,1]称为f的
的点x∈[0,1]称为f的 阶周期点.设
阶周期点.设 则f的
则f的