题目内容
 如图所示,|
如图所示,|| AB |
| AC |
| AO |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据题中数据,在△ABC中利用余弦定理算出BC=
,△ABC面积为S=
.算出内切圆的半径r=
.设内切圆与AC的切点为D,连结OD,可得∠OAD=60°.Rt△AOD中利用三角函数的定义算出AO=3-
,再根据向量数量积的定义加以计算,可得
•
的值.
| 7 |
| ||
| 2 |
| ||
|
| 7 |
| AO |
| AC |
解答:解: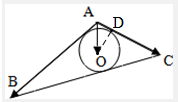 ∵△ABC中,AB=2,AC=1,∠BAC=120°,
∵△ABC中,AB=2,AC=1,∠BAC=120°,
∴根据余弦定理,得BC=
=
.
△ABC面积为S=
AB•AC•sin∠BAC=
×2×1×
=
,
设△ABC内切圆的半径为r,
可得S=
(AB+BC+CA)r=
,
即
(2+
+1)r=
,
解得r=
,
设内切圆与AC的切点为D,连结OD,
∵AO平分∠BAC,∠BAC=120°,
∴∠OAD=60°,
Rt△AOD中,AO=
=
=
=3-
,
因此,
•
=
•
•cos∠OAC=(3-
)•1•cos60°=
.
故选:B
 ∵△ABC中,AB=2,AC=1,∠BAC=120°,
∵△ABC中,AB=2,AC=1,∠BAC=120°,∴根据余弦定理,得BC=
| AB2+AC2-2AB•ACcos120° |
| 7 |
△ABC面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
设△ABC内切圆的半径为r,
可得S=
| 1 |
| 2 |
| ||
| 2 |
即
| 1 |
| 2 |
| 7 |
| ||
| 2 |
解得r=
| ||
|
设内切圆与AC的切点为D,连结OD,
∵AO平分∠BAC,∠BAC=120°,
∴∠OAD=60°,
Rt△AOD中,AO=
| OD |
| sin∠OAD |
| r |
| sin60° |
| 2 | ||
|
| 7 |
因此,
| AO |
| AC |
| |AO| |
| |AC| |
| 7 |
3-
| ||
| 2 |
故选:B
点评:本题给出△ABC的内切圆心为O,求
•
的值.着重考查了利用余弦定理解三角形、三角形的面积公式、三角形内切圆的性质和向量数量积计算公式等知识,属于中档题.
| AO |
| AC |

练习册系列答案
相关题目
 22、如图所示,AB为⊙O的直径,BC、CD为⊙O的切线,B、D为切点.
22、如图所示,AB为⊙O的直径,BC、CD为⊙O的切线,B、D为切点.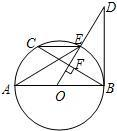 如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB. 选修4-1:几何证明选讲
选修4-1:几何证明选讲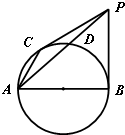 (2012•丰台区二模)如图所示,AB是圆的直径,点C在圆上,过点B,C的切线交于点P,AP交圆于D,若AB=2,AC=1,则PC=
(2012•丰台区二模)如图所示,AB是圆的直径,点C在圆上,过点B,C的切线交于点P,AP交圆于D,若AB=2,AC=1,则PC=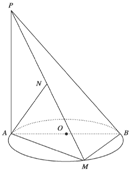 如图所示,AB是圆O的直径,PA垂直于圆O所在的平面,M是圆周上异于A、B的任意一点,AN⊥PM,点N为垂足,求证:AN⊥平面PBM.
如图所示,AB是圆O的直径,PA垂直于圆O所在的平面,M是圆周上异于A、B的任意一点,AN⊥PM,点N为垂足,求证:AN⊥平面PBM.