题目内容
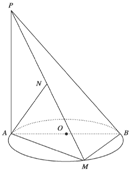如图所示，AB是圆O的直径，PA垂直于圆O所在的平面，M是圆周上异于A、B的任意一点，AN⊥PM，点N为垂足，求证：AN⊥平面PBM．分析：由圆周角定理可得AM⊥BM，由线面垂直的性质，可得PA⊥BM，进而由线面垂直的判定定理可得BM⊥平面PAM，得到AN⊥BM，
结合面面垂直的判定定理可得AN⊥平面PBM．
结合面面垂直的判定定理可得AN⊥平面PBM．
解答：证明：∵AB是圆的直径，M是圆周上异于A、B的任意一点，
∴AM⊥BM，
∵PA⊥平面ABM，BM?平面ABM，
∴PA⊥BM．
又∵PA∩AM=A，PA?平面PAM，AC?平面PAM，
∴BM⊥平面PAM，
又∵AN?平面PAM，
∴AN⊥BM，
又∵AN⊥PM，BM∩PM=M．
∴AN⊥平面PBM．
∴AM⊥BM，
∵PA⊥平面ABM，BM?平面ABM，
∴PA⊥BM．
又∵PA∩AM=A，PA?平面PAM，AC?平面PAM，
∴BM⊥平面PAM，
又∵AN?平面PAM，
∴AN⊥BM，
又∵AN⊥PM，BM∩PM=M．
∴AN⊥平面PBM．
点评：本题考查的知识点是直线与平面垂直的判定，其中熟练掌握空间线线垂直，线面垂直，面面垂直的相互转化是解答的关键．
练习册系列答案
相关题目
（几何证明选讲选做题）
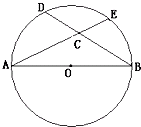
7、如图所示，AB是圆O的直径，C是异于A，B两点的圆周上的任意一点，PA垂直于圆O所在的平面，则△PAB，△PAC，△ABC，△PBC中，直角三角形的个数是（ ）
14、如图所示，AB是圆O的直径，C是异于A，B两点的圆周上的任意一点，PA垂直于圆O所在的平面，则△PAB，△PAC，△ABC，△PBC中，直角三角形的个数是
