题目内容
已知函数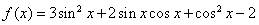 .
.
(Ⅰ)求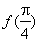 的值;
的值;
(Ⅱ)求函数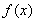 的最小正周期及单调递增区间.
的最小正周期及单调递增区间.
【答案】
(Ⅰ)1;(Ⅱ)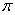 、
、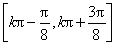 ,
,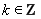
【解析】
试题分析:(Ⅰ)将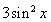 分解为
分解为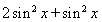 ,前者用余弦二倍角降幂,或者和
,前者用余弦二倍角降幂,或者和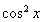 相加和为1。
相加和为1。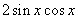 用正弦二倍角公式化为
用正弦二倍角公式化为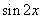 ,最后在用化一公式化简。在代入角求值。(Ⅱ)由(Ⅰ)知
,最后在用化一公式化简。在代入角求值。(Ⅱ)由(Ⅰ)知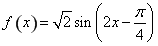 ,根据周期公式
,根据周期公式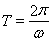 ,求其周期。将
,求其周期。将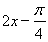 整体代入正弦增区间,求
整体代入正弦增区间,求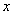 的取值范围,即为函数
的取值范围,即为函数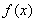 增区间。
增区间。
试题解析:(Ⅰ)依题意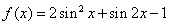
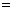
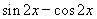
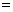
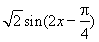 .
.
则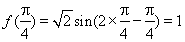 . 7分
. 7分
(Ⅱ)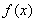 的最小正周期
的最小正周期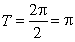 .
.
当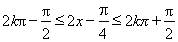 时,即
时,即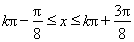 时,
时,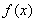 为增函数.
为增函数.
则函数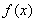 的单调增区间为
的单调增区间为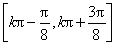 ,
,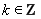 . .13分
. .13分
考点:(1)三角函数的基本关系式、二倍角公式,化一公式。(2)正弦的周期公式和单调性。

练习册系列答案
相关题目
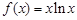 .
.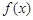 的最小值;
的最小值;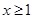 都有
都有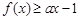 ,求实数
,求实数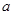 的取值范围.
的取值范围.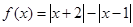
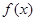 的值域;
的值域;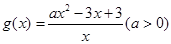 ,若对
,若对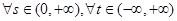 恒有
恒有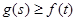 成立,试求实数
成立,试求实数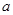 的取值氛围。
的取值氛围。 ,(1)求
,(1)求 的定义域;
的定义域; 是第四象限的角,且
是第四象限的角,且 ,求
,求 的值。
的值。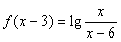 ,
,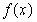 的解析式;
的解析式; .
.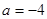 时,求
时,求 的最小值;
的最小值;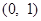 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;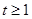 时,不等式
时,不等式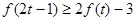 恒成立,求实数
恒成立,求实数