题目内容
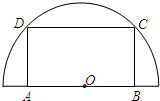 (2013•闵行区二模)如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
(2013•闵行区二模)如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.(1)请你在下列两个小题中选择一题作答即可:
①设∠BOC=θ,矩形ABCD的面积为S=g(θ),求g(θ)的表达式,并写出θ的范围.
②设BC=x(cm),矩形ABCD的面积为S=f(x),求f(x)的表达式,并写出x的范围.
(2)怎样截取才能使截得的矩形ABCD的面积最大?并求最大面积.
分析:(1)①连接OC,设∠BOC=θ,矩形ABCD的面积为S,则S=AB•BC=2OB•BC=900sin2θ,由三角函数的知识,得出S的最大值以及对应BC的值.
②连接OC,设BC=x,矩形ABCD的面积为S;则S=AB•BC=2x
=2
,由基本不等式可得S的最大值以及对应的x的取值;
(2)根据(1)问的解答,即可得出怎样截取才能使截得的矩形ABCD的面积最大及最大值.
②连接OC,设BC=x,矩形ABCD的面积为S;则S=AB•BC=2x
| 400-x2 |
| x2(400-x2) |
(2)根据(1)问的解答,即可得出怎样截取才能使截得的矩形ABCD的面积最大及最大值.
解答: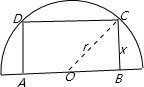 解:如图所示,
解:如图所示,
(1)①连接OC,设∠BOC=θ,矩形ABCD的 面积为S,则BC=30sinθ,OB=30cosθ(其中0<θ<
);
∴S=AB•BC=2OB•BC=900sin2θ,且当sin2θ=1,即θ=
时,S取最大值为900,此时BC=10
;
所以,取BC=10
时,矩形ABCD的面积最大,最大值为400cm2.
②连接OC,设BC=x,矩形ABCD的面积为S;则AB=2
(其中0<x<30),
∴S=2x
=2
≤x2+(400-x2)=400,当且仅当x2=400-x2,即x=10
时,S取最大值400;
所以,取BC=10
cm时,矩形ABCD的面积最大,最大值为400cm2.
(2)由(1)知,取∠BOC=
时,得到C点,从而截得的矩形ABCD,此时截得的矩形ABCD的面积最大,最大值为400cm2.
 解:如图所示,
解:如图所示,(1)①连接OC,设∠BOC=θ,矩形ABCD的 面积为S,则BC=30sinθ,OB=30cosθ(其中0<θ<
| π |
| 2 |
∴S=AB•BC=2OB•BC=900sin2θ,且当sin2θ=1,即θ=
| π |
| 4 |
| 2 |
所以,取BC=10
| 2 |
②连接OC,设BC=x,矩形ABCD的面积为S;则AB=2
| 400-x2 |
∴S=2x
| 400-x2 |
| x2(400-x2) |
| 2 |
所以,取BC=10
| 2 |
(2)由(1)知,取∠BOC=
| π |
| 4 |
点评:本题综合考查了二次函数、三角函数的最值问题,这里应用了基本不等式的方法求出了函数的最值.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目