题目内容
已知数列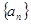 的各项均为正数,Sn为其前n项和,对于任意
的各项均为正数,Sn为其前n项和,对于任意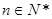 ,满足关系
,满足关系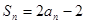 .
.
(Ⅰ)证明: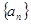 是等比数列;
是等比数列;
(Ⅱ)在正数数列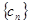 中,设
中,设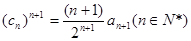 ,求数列
,求数列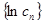 中的最大项.
中的最大项.
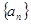 的各项均为正数,Sn为其前n项和,对于任意
的各项均为正数,Sn为其前n项和,对于任意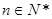 ,满足关系
,满足关系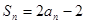 .
. (Ⅰ)证明:
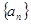 是等比数列;
是等比数列;(Ⅱ)在正数数列
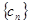 中,设
中,设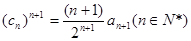 ,求数列
,求数列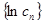 中的最大项.
中的最大项. (1)根据数列的定义,只要证明从第二项起,每一项与前面一项的比值为定值即可。(2)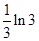
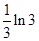
试题分析:(Ⅰ)证明:∵
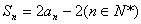 ①
①∴
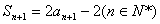 ②
② ②-①,得
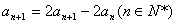
∵
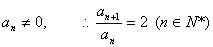 故数列
故数列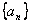 是等比数列
是等比数列(1)由Sn=2an-2(n∈N*),知Sn-1=2an-1-2(n≥2,n∈N*),所以an=2an-2an-1.(n≥2,n∈N*),由此可知an=2n.(n∈N*).
(2)令
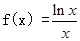 ,∵在区间(0,e)上,f'(x)>0,在区间(e,+∞)上,f'(x)<0.在区间(e,+∞)上f(x)为单调递减函数.(12分)
,∵在区间(0,e)上,f'(x)>0,在区间(e,+∞)上,f'(x)<0.在区间(e,+∞)上f(x)为单调递减函数.(12分)∴n≥2且n∈N*时,|lncn|是递减数列.又lnc1<lnc2,∴数列|lncn|中的最大项为lnc2=
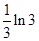
点评:该试题属于常规试题,主要是根据已知的关系式,变形为关于通项公式之间的递推关系,加以证明,属于基础题。

练习册系列答案
相关题目
 ,则第四项为( )
,则第四项为( )
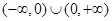 上的函数
上的函数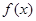 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列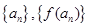 仍是等比数列,则称
仍是等比数列,则称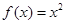 ;②
;②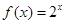 ;③
;③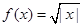 ;④
;④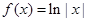 。则其中是“保等比数列函数”的
。则其中是“保等比数列函数”的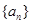 满足
满足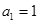 ,
,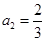 ,且
,且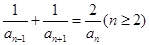 ,则
,则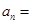
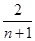

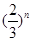
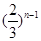
 满足
满足 ,则
,则 ( )
( )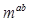 <1,则m的取值范围是( )
<1,则m的取值范围是( )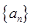 中,已知
中,已知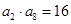 ,则
,则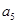 的值为( )
的值为( )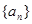 是公差不为零的等差数列,
是公差不为零的等差数列, 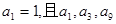 成等比数列.
成等比数列.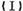 求数列
求数列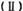 求数列
求数列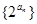 的前n项和
的前n项和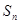
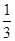 为第三项,9为第六项的等比数列的公比,则这个三角形是
为第三项,9为第六项的等比数列的公比,则这个三角形是