题目内容
如图,在一个可以向下和向右方无限延伸的表格中,将正偶数按已填好的各个方格中的数字显现的规律填入各方格中.其中第 行,第
行,第 列的数记作
列的数记作 ,
, ,如
,如 .
.
(I)写出 的值;
的值;
(II) 若 求
求 的值;(只需写出结论)
的值;(只需写出结论)
(III)设 ,
, (
( ), 记数列
), 记数列 的前
的前 项和为
项和为 ,求
,求 ;并求正整数
;并求正整数 ,使得对任意
,使得对任意 ,均有
,均有 .
.
| 2 | 4 | 8 | 14 | … |
| 6 | 10 | 16 | 24 | … |
| 12 | 18 | 26 | 36 | … |
| 20 | 28 | 38 | 50 | … |
| … | … | … | … | … |
解:(I) ,
, . ……………4分
. ……………4分
(II) I =20 , j =3. …………8分
(III)位于从左上角到右下角的对角线上的方格内的数字组成的数列是 2,10,26,50, bn 是依(II)中排法的第2 n – 1组的中间一个数,即第n个数,
所以 bn = ( 2n – 1 ) 2 n– 2 ( n – 1 ) = 4 n2 – 4 n + 2=4n ( n -1) + 2,n = 1,2,3,…;
因为  所以
所以 ,
,
故  .…………10分
.…………10分
因为  ;当
;当 时,
时, ,
,
而

得 ,
,
所以当 时,
时, ,综上对任意
,综上对任意 恒有
恒有 ,故
,故 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
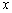 的不等式
的不等式 的解集为
的解集为 ,则
,则 _________.
_________. 的终边经过点(-3,4),则cos
的终边经过点(-3,4),则cos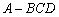 满足下列条件:
满足下列条件: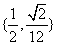 B.
B.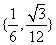 C.
C.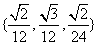 D.
D.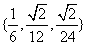
 的部分图象如图所示.
的部分图象如图所示. (I)求函数
(I)求函数 的解析式;
的解析式;
 )为其终边上一点且cos α=
)为其终边上一点且cos α= x,则x的值为( )
x,则x的值为( ) B.±
B.±

 在曲线
在曲线 上移动,设点
上移动,设点 ,则
,则 .[0,
.[0, ]
]  .[0,
.[0,
 .[
.[ ,π]
,π]  .[0,
.[0, ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.