题目内容
已知函数 的部分图象如图所示.
的部分图象如图所示.
 (I)求函数
(I)求函数 的解析式;
的解析式;
(II)求函数
的单调递增区间.
解:(I)由题意可知, ,
,
 ,得
,得 ,
, ,解得
,解得 .
.
 ,
,
即 ,
, ,
,
所以  ,故
,故 . ……………7分
. ……………7分
(II) 

由 

故
 . ……………13分
. ……………13分

练习册系列答案
相关题目
如图,在一个可以向下和向右方无限延伸的表格中,将正偶数按已填好的各个方格中的数字显现的规律填入各方格中.其中第 行,第
行,第 列的数记作
列的数记作 ,
, ,如
,如 .
.
(I)写出 的值;
的值;
(II) 若 求
求 的值;(只需写出结论)
的值;(只需写出结论)
(III)设 ,
, (
( ), 记数列
), 记数列 的前
的前 项和为
项和为 ,求
,求 ;并求正整数
;并求正整数 ,使得对任意
,使得对任意 ,均有
,均有 .
.
| 2 | 4 | 8 | 14 | … |
| 6 | 10 | 16 | 24 | … |
| 12 | 18 | 26 | 36 | … |
| 20 | 28 | 38 | 50 | … |
| … | … | … | … | … |
 的取值如表所示
的取值如表所示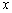

 线性相关,且线性回归方程为
线性相关,且线性回归方程为 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 为等差数列,满足
为等差数列,满足 ,则数列
,则数列 B.21 C.42 D.84
B.21 C.42 D.84 的公差是2,若
的公差是2,若 成等比数列,则
成等比数列,则  等于
等于 B.
B.  C.
C.  D.
D. 
 _______,
_______, .
.


 在
在 处的导数
处的导数 的几何意义是( ).
的几何意义是( ). .在点
.在点 处的斜率;
处的斜率;  .曲线
.曲线 处切线的斜率;
处切线的斜率; .在点
.在点 轴所夹锐角的正切值;
轴所夹锐角的正切值; .点
.点 连线的斜率.
连线的斜率. 的参数方程为
的参数方程为 (其中
(其中 为参数),点M是曲线
为参数),点M是曲线 上,且满足
上,且满足
 轴的正半轴为极轴建立极坐标系,射线分别交于
轴的正半轴为极轴建立极坐标系,射线分别交于 与曲线
与曲线 分别交于A、B两点,求
分别交于A、B两点,求