题目内容
若函数 和y=|x+a|的图象有三个不同的公共点,则实数a的取值范围是
和y=|x+a|的图象有三个不同的公共点,则实数a的取值范围是
- A.a≥-4
- B.a<-4
- C.a≤4
- D.a>4
B
分析:首先根据函数的表达式画出函数的图象,从而根据图象判断函数与直线的公共点的情况,最后结合两曲线相切与方程有唯一解的关系即可求得实数a的取值范围.
解答: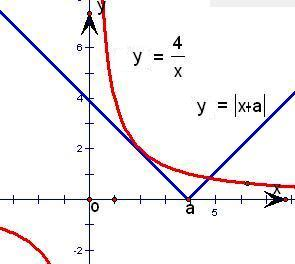 解:画出函数数
解:画出函数数 和y=|x+a|的图象,(如图).
和y=|x+a|的图象,(如图).
由图可知,当且仅当直线y=a+x与函数 的图象相切时,
的图象相切时,
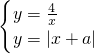 有唯一解,∴a=-4,
有唯一解,∴a=-4,
函数 和y=|x+a|的图象有三个不同的公共点,则实数a的取值范围是a<-4
和y=|x+a|的图象有三个不同的公共点,则实数a的取值范围是a<-4
故选B.
点评:本题主要考查函数的零点以及数形结合方法,数形结合是数学解题中常用的思想方法,本题由于使用了数形结合的方法,使得问题便迎刃而解,且解法简捷.
分析:首先根据函数的表达式画出函数的图象,从而根据图象判断函数与直线的公共点的情况,最后结合两曲线相切与方程有唯一解的关系即可求得实数a的取值范围.
解答:
 解:画出函数数
解:画出函数数 和y=|x+a|的图象,(如图).
和y=|x+a|的图象,(如图).由图可知,当且仅当直线y=a+x与函数
 的图象相切时,
的图象相切时,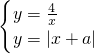 有唯一解,∴a=-4,
有唯一解,∴a=-4,函数
 和y=|x+a|的图象有三个不同的公共点,则实数a的取值范围是a<-4
和y=|x+a|的图象有三个不同的公共点,则实数a的取值范围是a<-4故选B.
点评:本题主要考查函数的零点以及数形结合方法,数形结合是数学解题中常用的思想方法,本题由于使用了数形结合的方法,使得问题便迎刃而解,且解法简捷.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(文科)若函数y=
和y=|x-a|的图象有三个不同的公共点,则实数a的取值范围是( )
| 4 |
| x |
| A、a>-4 | B、a≤-4 |
| C、a≤4 | D、a>4 |
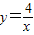 和y=|x+a|的图象有三个不同的公共点,则实数a的取值范围是( )
和y=|x+a|的图象有三个不同的公共点,则实数a的取值范围是( ) 和y=|x-a|的图象有三个不同的公共点,则实数a的取值范围是( )
和y=|x-a|的图象有三个不同的公共点,则实数a的取值范围是( )