题目内容
已知O为△ABC所在平面外一点,且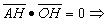 .
.
解:由![]() ,连AH并延长交BC于M.
,连AH并延长交BC于M.
则由H为△ABC的垂心.∴AM⊥BC.
于是BC⊥平面OAH![]() OH⊥BC.
OH⊥BC.
同理可证:![]()
又![]() 是空间中三个不共面的向量,由向量基本定理知,存在三个实数k1,k2,k3使得
是空间中三个不共面的向量,由向量基本定理知,存在三个实数k1,k2,k3使得![]() =k1a+k2b+k3c.
=k1a+k2b+k3c.
由![]() =0且a·b=a·c=0
=0且a·b=a·c=0![]() k2b2=k3c2,同理k1a2=k2b2.
k2b2=k3c2,同理k1a2=k2b2.
∴k1a2=k2b2=k3c2=m≠0.①又AH⊥OH,
∴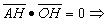
(k1-1)a+k2b+k3c(k1a+k2b+k3c)=0![]() k1(k1-1)a2+k22b2+k32c2=0②?
k1(k1-1)a2+k22b2+k32c2=0②?
联立①及②,得
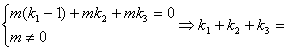 1③
1③
又由①,得k1=![]() ,k2=
,k2=![]() ,k3=
,k3=![]() ,代入③得
,代入③得
m=![]()
![]()
![]() ,?
,?
其中Δ=a2·b2+b2·c2+c2·a2,于是![]() =
=![]() (b2·c2·a+c2·a2·b+a2·b2·c).
(b2·c2·a+c2·a2·b+a2·b2·c).

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
已知O为△ABC所在平面内一点,满足|
|2+|
|2=|
|2+|
|2=|
|2+|
|2,则点O是△ABC的( )
| OA |
| BC |
| OB |
| CA |
| OC |
| AB |
| A、外心 | B、内心 | C、垂心 | D、重心 |
 ,则点O是△ABC的(
)
,则点O是△ABC的(
)