题目内容

16．已知正方形ABCD的顶点坐标分别为A（0，1），B（2，0），C（3，2）．
（1）求CD边所在直线的方程；
（2）求以AC为直径的圆M的标准方程．

分析 （1）求出AB的斜率，利用点斜式求CD边所在直线的方程；
（2）圆心显然应在AC的中点处，求出圆的半径，即可求以AC为直径的圆M的标准方程．

解答 解：（1）由题意kAB=-$\frac{1}{2}$…3分
直线CD平行于AB，且过C（3，2），
所以直线CD的方程为y-2=-$\frac{1}{2}$（x-3），即x+2y-7=0；…6分
（2）圆心显然应在AC的中点处，记为M（$\frac{3}{2}$，$\frac{3}{2}$），…8分
R=MA=$\sqrt{\frac{9}{4}+\frac{1}{4}}$=$\sqrt{\frac{5}{2}}$，…10分
所以圆M的标准方程为（x-$\frac{3}{2}$）2+（y-$\frac{3}{2}$）2=$\frac{5}{2}$．…12分．

点评 本题考查直线与圆的方程，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
6．在△ABC中，a，b，c分别为内角A，B，C的对边，5a2-5c2=5b2-8bc，边b，c是关于x的方程：x2-（12tanA）x+25cosA=0的两个根（b＜c），D为△ABC内任一点，点D到三边的距离和为d．
（1）求边a，b，c；
（2）求d的取值范围．
7．等差数列{an}中，a4=20，a6=12，则{an}的前9项和S9=144．
4．如图，将边长为$\sqrt{2}$的正方形ABCD沿对角线BD折起，使得AC=1，则三棱锥A-BCD的体积为（　　）
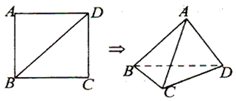
A．$\frac{{\sqrt{3}}}{6}$B．$\frac{{\sqrt{3}}}{3}$C．$\frac{{\sqrt{3}}}{2}$D．$\frac{1}{3}$
11．在数列{an}中，a1=1，an+1=$\frac{{a}_{n}}{c•{a}_{n}+1}$ （c为常数，n∈N*）且a5=a22，
（1）求证：数列{$\frac{1}{{a}_{n}}$}是等差数列；
（2）求c的值；
（3）若a1，a2，a5彼此不相等，数列{an•bn}是首项为1，公比为$\frac{1}{2}$的等比数列，求：数列{bn}的前n项和为Sn．
1．实数x，y满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤1\\ y≥0\end{array}\right.$，则z=2x+y最大值为（　　）
A．0B．1C．2D．$\frac{3}{2}$
8．若y=f（x）是定义在R上的函数，f（x+2）=-f（x），当0≤x≤2时，f（x）=4x+$\frac{3}{x}$，则f（5）=7．
5．已知函数$f（x）=\frac{1}{{{4^x}-1}}+2a$是奇函数
（1）求常数a的值
（2）判断函数f（x）在区间（-∞，0）上的单调性，并给出证明．
6．某四棱柱的三视图如图所示，则该四棱柱的体积为（　　）
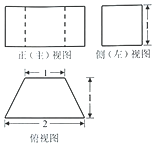
A．$\frac{5}{4}$B．$\frac{3}{2}$C．$\frac{5}{2}$D．$\frac{{\sqrt{3}}}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网