Question

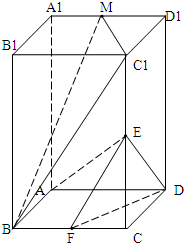已知正四棱柱ABCD-A₁B₁C₁D₁中AA1=2AB，E、F、M分别为CC₁、BC、A₁D₁中点．
（1）求证：AE∥面BC₁M；
（2）求二面角F-ED-A的余弦值．

Answer 1

分析：法一：（1）通过证明面AEF∥面BC₁M来证明AE∥面BC₁M；
（2）分别取AE，ED中点O，O′．先根据条件得到四边形FCO′O为平行四边形，进而得FO∥CO′；再通过CO′⊥面AED得到∠OO′F为二面角F-ED-A平面角，最后通过求三角形的边长求出角的函数值即可．
法二：（1）转化为证明平面BC₁M的法向量

a

与

AE

的数量积为0；
（2）分别求出两个半平面的法向量，再代入向量的夹角计算公式即可．

解答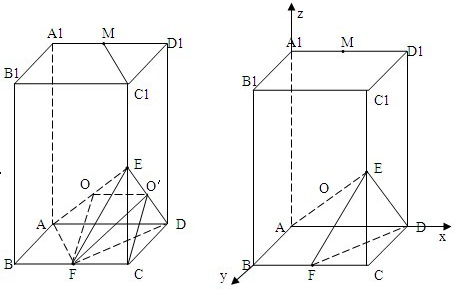：法一：（1）证：E，F为CC₁，BC中点⇒EF∥BC₁⇒EF∥面BC₁M
F，M为BC，A₁D₁中点⇒AF∥C₁M⇒AF∥面BC₁M
⇒面AEF∥面BC₁M⇒AE∥面BC₁M
（2）分别取AE，ED中点O，O′．连接FO，CO′，OO′，则OO′∥

1

2

AD∥FC
∴平行四边形FCO′O
∴FO∥CO′
∵EC=CE
∴CO′⊥ED⇒CO′⊥面AED
AD⊥面CD D₁C₁⇒AD⊥CO′⇒FO⊥面AED
∵OO′⊥ED．
连接O′F．则O′F⊥ED
∴∠OO′F为二面角F-ED-A平面角，
不妨设AB=1  AA′=2
在Rt△FOO′中，OO′=

1

2

AD=

1

2

，AF=AE=

5

2

，
AE=

3

∴FO=

2

2

∴tan∠OO′F=

FO

OO′

=

2

∠OO′F=arctan

2

∴二面角为arctan

2

．
法二：建立如图坐标系，不妨设AA₁=2AB=4．则

AE

=（2，2，2）
（1）设平面BC₁M的法向量为

a

，则：

BC1 • a =0 C1M  • a =0

⇒

a

=（2，-1，-1）
∵

AB

•

a

=0∴

AE

⊥

a

∴

AE

∥面BC₁M
（2）同理，可解得面ADE的法向量=（0，1，-1）面FED的法向量=（-2，-1，1）
∴cos（

C

•

a

=

c • d

| c | | d |

=

-2

2 • 6

=-

3

3

显然二面角F-ED-A为锐二面角
∴二面角F-ED-A为arccos

3

3

．

点评：本题主要考察二面角的平面角及求法．解决这类问题用空间向量的做法的关键是求出两个半平面的法向量，再代入向量的夹角计算公式．