题目内容
已知函数f（x0）=ln（x+
，则f′（x）是
- A.奇函数
- B.偶函数
- C.非奇非偶函数
- D.既奇又偶函数
B
分析：先设出内函数，利用复合函数的导数公式求出f′（x），求出f′（-x）得到f′（x）=f′（-x），利用偶函数的定义得到导函数为偶函数．
解答：令u=x+，则
y=lnu，
所以y′=（lnu）′（x+）′
=
=
=
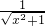
即f′（x）=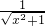
所以f′（-x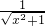）==f′（x）
所以函数为偶函数，
故选B．
点评：本题考查复合函数的导数公式：内函数与外函数的乘积，考查函数奇偶性的判断，属于基础题．
分析：先设出内函数，利用复合函数的导数公式求出f′（x），求出f′（-x）得到f′（x）=f′（-x），利用偶函数的定义得到导函数为偶函数．
解答：令u=x+
，则y=lnu，
所以y′=（lnu）′（x+
）′=
=
=
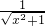
即f′（x）=
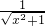
所以f′（-x）=
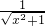=f′（x）所以函数为偶函数，
故选B．
点评：本题考查复合函数的导数公式：内函数与外函数的乘积，考查函数奇偶性的判断，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目