题目内容
（文）函数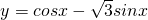
的图象的对称轴是
- A.
- B.
- C.
- D.
C
分析：将函数y解析式提取2，利用特殊角的三角函数值及两角和与差的余弦函数公式化为一个角的余弦函数，根据余弦函数的对称轴为x=kπ（k∈Z），对于四个选项进行检验，即可得到正确的选项．
解答：y=cosx-
sinx=2（
cosx-
sinx）=2cos（x+），
令x+=kπ（k∈Z），解得：x=kπ-（k∈Z），
当kπ-=，解得：k=，不合题意，舍去；
当kπ-=，解得：k=
，不合题意，舍去；
当kπ-=，解得：k=1，符合题意，
当kπ-=，解得：k=
，不合题意，舍去，
则函数y图象的对称轴是x=．
故选C
点评：此题考查了两角和与差的余弦函数公式，以及余弦函数的对称性，其中将函数解析式化为一个角的余弦函数是本题的突破点．
分析：将函数y解析式提取2，利用特殊角的三角函数值及两角和与差的余弦函数公式化为一个角的余弦函数，根据余弦函数的对称轴为x=kπ（k∈Z），对于四个选项进行检验，即可得到正确的选项．
解答：y=cosx-
sinx=2（cosx-sinx）=2cos（x+），令x+
=kπ（k∈Z），解得：x=kπ-（k∈Z），当kπ-
=，解得：k=，不合题意，舍去；当kπ-
=，解得：k=，不合题意，舍去；当kπ-
=，解得：k=1，符合题意，当kπ-
=，解得：k=，不合题意，舍去，则函数y图象的对称轴是x=
．故选C
点评：此题考查了两角和与差的余弦函数公式，以及余弦函数的对称性，其中将函数解析式化为一个角的余弦函数是本题的突破点．
练习册系列答案
相关题目
N
)都在函数
的图象上.
是等差数列,求证数列
为等比数列；
项和为
=
,过点
的直线与两坐标轴所围成三角
,求使
对
N
的取值范围.
其导函数
的图象经过点
,且
在
时取得极小值-8.
都有
恒成立，求实数
的取值范围。
的前
项和为
，对一切
，点
在函数
的图象上.
的表达式；
），（
，
），（
，
，
），（
，
，
，
）；（
），（
，
），(
，
，
），（
，
，
，
）；（
），…，分别计算各个括号内各数之和，设由这些和按原来括号的前后顺序构成的数列为
，求
的值；
为数列
的前
，使得不等式
对一切
满足条件：
，均有
；②函数
的图象与直线
相切
时，
恒成立，试求
的值。
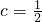时，求出不等式f（x）＜0的解；