题目内容
若M为△ABC所在平面内一点,且满足(
-
)•(
+
)=0,
+
+2
=
,则△ABC的形状为( )
| MB |
| MC |
| MB |
| MC |
| MB |
| MC |
| MA |
| 0 |
分析:根据(
-
)•(
+
)=0算出△MBC中MB=MC,△MBC是等腰三角形.而
+
+2
=
,得到
+
=-2
,代入第一个等式可得
•2
=0,从而得到BC⊥AM.再根据△MBC是等腰三角形,得到AM是BC的垂直平分线,可得AB=AC,而且M不是△ABC的重心,可得△ABC是等腰三角形且不是等边三角形,得到本题答案.
| MB |
| MC |
| MB |
| MC |
| MB |
| MC |
| MA |
| 0 |
| MB |
| MC |
| MA |
| CB |
| MA |
解答: 解:∵(
解:∵(
-
)•(
+
)=0
∴
2-
2=|
|2-|
|2=0,可得|
|=|
|
由此可得△MBC中MB=MC,△MBC是等腰三角形
又∵
+
+2
=
,可得
+
=-2
∴结合(
-
)•(
+
)=0,得
•2
=0
由此可得BC所在直线与AM所在直线互相垂直,
∵AM与等腰△BMC的底边中线ME在一条直线上,
∴AM是BC的垂直平分线,可得AB=AC,得△ABC是等腰三角形
又∵
+
=-2
,∴△ABC不是等边三角形
故选:B
 解:∵(
解:∵(| MB |
| MC |
| MB |
| MC |
∴
| MB |
| MC |
| MB |
| MC |
| MB |
| MC |
由此可得△MBC中MB=MC,△MBC是等腰三角形
又∵
| MB |
| MC |
| MA |
| 0 |
| MB |
| MC |
| MA |
∴结合(
| MB |
| MC |
| MB |
| MC |
| CB |
| MA |
由此可得BC所在直线与AM所在直线互相垂直,
∵AM与等腰△BMC的底边中线ME在一条直线上,
∴AM是BC的垂直平分线,可得AB=AC,得△ABC是等腰三角形
又∵
| MB |
| MC |
| MA |
故选:B
点评:本题给出三角形中的向量式,叫我们判断三角形的形状,着重考查了平面向量的数量积计算性质和向量加减法的定义等知识,属于中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
若M为△ABC所在平面内一点,且满足(
-
)•(
+
-2
=0,则△ABC的形状为( )
| MB |
| MC |
| MB |
| MC |
| MA) |
| A、正三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
若M为△ABC所在平面内一点,且满足|
-
|=|
+
-2MA|,则△ABC的形状为( )
| MB |
| MC |
| MB |
| MC |
| A、正三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
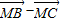 )•
)•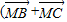 -2
-2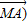 =0,则△ABC的形状为( )
=0,则△ABC的形状为( ) |=|
|=| |,则△ABC的形状为( )
|,则△ABC的形状为( )