题目内容
若M为△ABC所在平面内一点,且满足|
-
|=|
+
-2MA|,则△ABC的形状为( )
| MB |
| MC |
| MB |
| MC |
| A、正三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
分析:化简关于向量模的方程,根据向量模的几何意义,判定三角形的形状即可.
解答:解:|
-
|=|
+
-2MA|,
可得|
| =|
+
|,
它的几何意义是:以AB、AC为邻边的平行四边形的对角线相等,
所以AB⊥AC,
△ABC是直角三角形.
故选B.
| MB |
| MC |
| MB |
| MC |
可得|
| CB |
| AB |
| AC |
它的几何意义是:以AB、AC为邻边的平行四边形的对角线相等,
所以AB⊥AC,
△ABC是直角三角形.
故选B.
点评:本题考查平面向量数量积的运算,向量模的几何意义,考查计算推理能力,是基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
若M为△ABC所在平面内一点,且满足(
-
)•(
+
-2
=0,则△ABC的形状为( )
| MB |
| MC |
| MB |
| MC |
| MA) |
| A、正三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
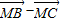 )•
)•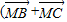 -2
-2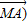 =0,则△ABC的形状为( )
=0,则△ABC的形状为( ) |=|
|=| |,则△ABC的形状为( )
|,则△ABC的形状为( )