题目内容
若M为△ABC所在平面内一点,且满足(
-
)•(
+
-2
=0,则△ABC的形状为( )
| MB |
| MC |
| MB |
| MC |
| MA) |
| A、正三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
分析:由(
-
)•(
+
-2
=0,可得
•(
-
+
-
)=0,即
•(
+
)=0,根据向量加法的平行四边形法则可求
| MB |
| MC |
| MB |
| MC |
| MA) |
| CB |
| MB |
| MA |
| MC |
| MA |
| CB |
| AB |
| AC |
解答:解:由(
-
)•(
+
-2
=0,可得
•(
-
+
-
)=0
•(
+
)=0
从而可得以
,
为临边坐平行四边形的对角线与
垂直
从而可得|
|=|
|
故选:C
| MB |
| MC |
| MB |
| MC |
| MA) |
| CB |
| MB |
| MA |
| MC |
| MA |
| CB |
| AB |
| AC |
从而可得以
| AB |
| AC |
| BC |
从而可得|
| AC |
| AB |
故选:C
点评:本题主要考查了利用向量的加法与减法的运算的平行四边形法则判断三角形的形状,解题的关键是要能利用基本法则看到
+
-2
的转换方法.
| MB |
| MC |
| MA |

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
若M为△ABC所在平面内一点,且满足|
-
|=|
+
-2MA|,则△ABC的形状为( )
| MB |
| MC |
| MB |
| MC |
| A、正三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
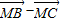 )•
)•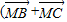 -2
-2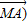 =0,则△ABC的形状为( )
=0,则△ABC的形状为( ) |=|
|=| |,则△ABC的形状为( )
|,则△ABC的形状为( )