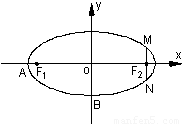
题目内容
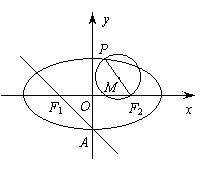 已知椭圆
已知椭圆 :
: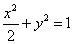 的左、右焦点分别为
的左、右焦点分别为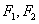 ,下顶点为
,下顶点为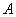 ,点
,点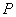 是椭圆上任一点,⊙
是椭圆上任一点,⊙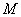 是以
是以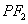 为直径的圆.
为直径的圆.
(Ⅰ)当⊙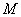 的面积为
的面积为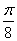 时,求
时,求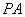 所在直线的方程;
所在直线的方程;
(Ⅱ)当⊙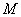 与直线
与直线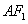 相切时,求⊙
相切时,求⊙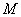 的方程;
的方程;
(Ⅲ)求证:⊙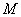 总与某个定圆相切.
总与某个定圆相切.

【答案】
解:(Ⅰ)易得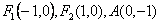 ,设点P
,设点P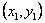 ,
,
则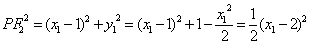 ,所以
,所以 …3分
…3分
又⊙ 的面积为
的面积为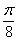 ,∴
,∴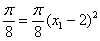 ,解得
,解得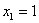 ,∴
,∴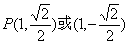 ,
,
∴ 所在直线方程为
所在直线方程为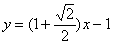 或
或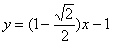 ………………5分
………………5分
(Ⅱ)因为直线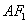 的方程为
的方程为 ,且
,且 到直线
到直线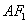 的
的
距离为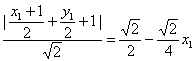 ………………………………7分
………………………………7分
化简,得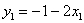 ,联立方程组
,联立方程组 ,解得
,解得 或
或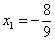 …10分
…10分
∴当 时,可得
时,可得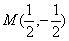 ,∴⊙
,∴⊙ 的方程为
的方程为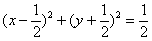 ;
;
当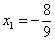 时,可得
时,可得 ,∴⊙
,∴⊙ 的方程为
的方程为 …12分
…12分
(Ⅲ)⊙ 始终和以原点为圆心,半径为
始终和以原点为圆心,半径为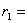
 (长半轴)的圆(记作⊙
(长半轴)的圆(记作⊙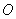 )相切13分
)相切13分
证明:因为
 ,
,
又⊙ 的半径
的半径
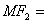
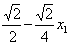 ,∴
,∴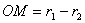 ,∴⊙
,∴⊙ 和⊙
和⊙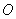 相内切…16分
相内切…16分
(说明:结合椭圆定义用几何方法证明亦可)

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:

 的方程为
的方程为  ,双曲线
,双曲线 的左、右焦
的左、右焦 与双曲线C2恒有两个不同的交点A和B,求
与双曲线C2恒有两个不同的交点A和B,求 的范围。
的范围。 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的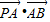 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.