题目内容
如果 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于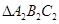 的三个内角的正弦值,则(
)
的三个内角的正弦值,则(
)
A. 和
和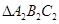 都是锐角三角形
都是锐角三角形
B. 和
和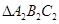 都是钝角三角形
都是钝角三角形
C. 是钝角三角形,
是钝角三角形,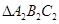 是锐角三角形
是锐角三角形
D. 是锐角三角形,
是锐角三角形,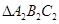 是钝角三角形
是钝角三角形
【答案】
D
【解析】
试题分析:因为三角形内角范围是(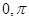 ),在此范围内,角的正弦均为正值,
),在此范围内,角的正弦均为正值,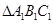 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于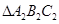 的三个内角的正弦值,所以
的三个内角的正弦值,所以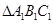 是锐角三角形。
是锐角三角形。
若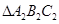 是锐角三角形,由
是锐角三角形,由 ,
,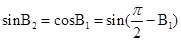 ,
, 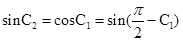 ,
,
得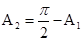 ,
, 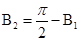 ,
, 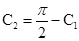 ,
,
那么,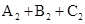 =
= 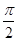 ,这与三角形内角和是π相矛盾;
,这与三角形内角和是π相矛盾;
若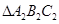 是直角三角形,不妨设
是直角三角形,不妨设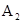 =
=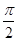 ,
,
则sin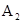 =1=cos
=1=cos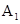 ,所以
,所以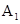 在(0,π)范围内无值.
在(0,π)范围内无值.
所以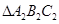 是钝角三角形.
是钝角三角形.
故选D.
考点:本题主要考查三角函数的诱导公式,三角形内角和定理,分类讨论思想。
点评:中档题,应用分类讨论思想,对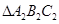 的可能情况进行讨论,通过排除锐角三角形、直角三角形的情况,肯定其为钝角三角形。
的可能情况进行讨论,通过排除锐角三角形、直角三角形的情况,肯定其为钝角三角形。

练习册系列答案
相关题目
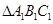 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 对应的三个内角的正弦值,则
对应的三个内角的正弦值,则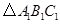 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 的三个内角的正弦值,则( )
的三个内角的正弦值,则( ) 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 的三个内角的正弦值,则( )
的三个内角的正弦值,则( ) 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 的三个内角的正弦值,则()
的三个内角的正弦值,则()
 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 的三个内角的正弦值,则
的三个内角的正弦值,则