题目内容
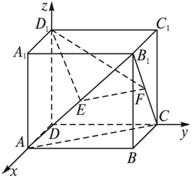
在正四棱柱ABCD—A1B1C1D1中,底面边长为
证明:把正四棱柱如图放置在坐标系中, 则各点坐标为A(![]() , 0, 0), C(0,
, 0, 0), C(0,![]() , 0), B1(
, 0), B1(![]() ,
,![]() ,
,![]() ), D1(0, 0,
), D1(0, 0,![]() ), E(
), E(![]() ,
,![]() ,
,![]() ), F(
), F(![]() ,
,![]() ,
,![]() ).假设平面AB1C的法向量为n1=(1, λ1, μ1), 则n1应垂直于
).假设平面AB1C的法向量为n1=(1, λ1, μ1), 则n1应垂直于![]() 和
和![]() .而
.而![]() ,
,![]() ,
,
∴![]() 及
及![]() .
.
∴λ1=1,![]() .∴n1=(1, 1,
.∴n1=(1, 1,![]() ).
).
再假设平面D1EF的法向量为n2=(1, λ2, μ2), 则n2应垂直于![]() 、
、![]() , 而
, 而![]() ,
,![]() ,
,
∴![]() ,
,
![]() .
.
∴λ2=1,![]() .∴n2=(1, 1,
.∴n2=(1, 1,![]() ).
).
由于n1 n2=1+1-
n2=1+1-![]() =1+1-2=0,
=1+1-2=0,
∴n1⊥n2.因此平面D1EF⊥平面AB1C.

练习册系列答案
相关题目
 如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点. 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点. 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点. (2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)
(2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)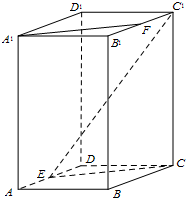 (2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.
(2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.