题目内容

函数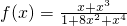 $数学公式$ 的最大值为________．

$\text{[math]}$
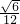
分析：由题意对函数求导，然后解f′（x）=0方程，得到x=-1或x=1，将（-∞，+∞）分为三个区间，最后通过列表得出导数在这三个区间的符号，讨论出函数的单调性，即可得出函数的最大最小值．
解答：由于函数f（x）的定义域为R
f'（x）= $\text{[math]}$
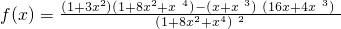
令f'（x）=0得x=-1或x=1列表：

x	（-∞，-1）	-1	（-1，1）	1	（1，∞）
f'（x）	-	0	₊	0	-
f（x）	↘	极小值	↗	极大值	↘

由上表可以得到
当x∈（-∞，-1）和x∈（1，+∞）时函数为减函数
当x∈（-1，1）时，函数为增函数
所以当x=-1时函数有极小值为-3；当x=1时函数有极大值为 $\text{[math]}$
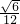
函数 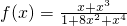$\text{[math]}$ 的最大值为 $\text{[math]}$ ．
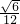点评：本题考查了函数的求导及极值的概念，其基本思路是利用导函数的零点求出可能的极值点，再利用表格讨论导数的正负，从而求其单调区间，最后得出函数的极值，这是典型的化归思想．