题目内容
下列命题中,真命题的个数为( )
(1)在△ABC中,若A>B,则sinA>sinB;
(2)已知
=(3,4),
=(-2,-1),则
在
上的投影为-2;
(3)函数的y=lg(x2+ax+1)的值域为R,则实数-2<a<2;
(4)已知函数f(x)=sin(ωx+
)-2(ω>0)的导函数的最大值为3,则函数f(x)的图象关于x=
对称.
(1)在△ABC中,若A>B,则sinA>sinB;
(2)已知
| AB |
| CD |
| AB |
| CD |
(3)函数的y=lg(x2+ax+1)的值域为R,则实数-2<a<2;
(4)已知函数f(x)=sin(ωx+
| π |
| 6 |
| π |
| 3 |
分析:根据正弦定理及三角形中“大边对大角”,可以判断(1)的真假;
根据向量投影的定义,计算出
在
上的投影,可判断(2)的真假;
根据对数函数的性质,其中函数的y=lg(x2+ax+1)的值域为R,则真数x2+ax+1的取值范围包含(0,+∞),则对应方程x2+ax+1=0有实根,可判断(3)的真假;
根据函数f(x)的导函数的最大值为3,求出ω值,将x=
代入判断是否此时函数取最值,可判断(4)的真假.
根据向量投影的定义,计算出
| AB |
| CD |
根据对数函数的性质,其中函数的y=lg(x2+ax+1)的值域为R,则真数x2+ax+1的取值范围包含(0,+∞),则对应方程x2+ax+1=0有实根,可判断(3)的真假;
根据函数f(x)的导函数的最大值为3,求出ω值,将x=
| π |
| 3 |
解答:解:在△ABC中,若A>B⇒a>b⇒2rsinA>2rsinB⇒sinA>sinB,故(1)正确;
∵
=(3,4),
=(-2,-1),则
在
上的投影为
=
=-2
,故(2)不正确;
函数的y=lg(x2+ax+1)的值域为R,则x2+ax+1=0有实根,即a2-4≥0则实数-2≤a≤2,故(3)不正确;
函数f(x)=sin(ωx+
)-2(ω>0)的导函数f′(x)=ω•cos(ωx+
)的最大值为3,则ω=3,当x=
时,函数f(x)=sin(3x+
)-2不取最值,故x=
不是函数f(x)的图象的对称轴,故(4)错误;
故选A
∵
| AB |
| CD |
| AB |
| CD |
| ||||
|
|
| -10 | ||
|
| 5 |
函数的y=lg(x2+ax+1)的值域为R,则x2+ax+1=0有实根,即a2-4≥0则实数-2≤a≤2,故(3)不正确;
函数f(x)=sin(ωx+
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
故选A
点评:本题以命题的真假判断为载体考查了正弦定理,向量的投影,对数函数的图象和性质,正弦型函数的图象和性质,其中(3)(4)较难

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
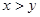 ,则
,则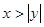 ”的逆命题
”的逆命题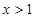 ,则
,则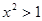 ”的否命题
”的否命题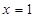 ,则
,则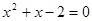 ”的否命题
”的否命题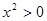 ,则
,则