题目内容
向面积为S的三角形ABC内任投一点P，则△PBC的面积小于
的概率是
．
| S |
| 3 |
| 5 |
| 9 |
| 5 |
| 9 |
分析：在三角形ABC内部取一点P，要满足得到的三角形PBC的面积是原三角形面积的
，根据几何关系求解出它们的比例即可．
| 1 |
| 3 |
解答：解：记事件A={△PBC的面积大于
}，
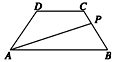
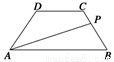
基本事件是三角形ABC的面积，（如图）
事件A的几何度量为图中阴影部分的面积（D、E分别是三角形的边上的三等分点），
∵△ADE∽△ABC，且相似比为
，
∴
=
，
∴阴影部分的面积是整个三角形面积的
，
∴P（A）=
=
，
∴△PBC的面积小于
的概率是1-P（A）=1-
=
．
故答案为：
．
| S |
| 3 |
基本事件是三角形ABC的面积，（如图）
事件A的几何度量为图中阴影部分的面积（D、E分别是三角形的边上的三等分点），
∵△ADE∽△ABC，且相似比为
| 2 |
| 3 |
∴
| S△ADE |
| S△ABC |
| 4 |
| 9 |
∴阴影部分的面积是整个三角形面积的
| 4 |
| 9 |
∴P（A）=
| 阴影部分的面积 |
| 三角形ABC的面积 |
| 4 |
| 9 |
∴△PBC的面积小于
| S |
| 3 |
| 4 |
| 9 |
| 5 |
| 9 |
故答案为：
| 5 |
| 9 |
点评：本题考查了几何概型，解答此题的关键在于明确测度比是面积比．对于几何概型常见的测度是长度之比，面积之比，体积之比，角度之比，要根据题意合理的判断和选择是哪一种测度进行求解．属于中档题．
练习册系列答案
相关题目
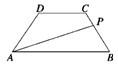等腰梯形ABCD的两底分别为AB=10，CD=4，两腰AD=CB=5，动点P由B点沿折线BCDA向A运动，设P点所经过的路程为x，三角形ABP的面积为S
（2013•湖北）如图，某地质队自水平地面A，B，C三处垂直向地下钻探，自A点向下钻到A1处发现矿藏，再继续下钻到A2处后下面已无矿，从而得到在A处正下方的矿层厚度为A1A2=d1．同样可得在B，C处正下方的矿层厚度分别为B1B2=d2，C1C2=d3，且d1＜d2＜d3．过AB，AC的中点M，N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面，其面积记为S中．
的解析式；