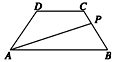
题目内容
等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S.
(1)求函数S=f(x)的解析式;
(2)试确定点P的位置,使△ABP的面积S最大.
(1)S=f(x)=
(2)当P点在CD上时,△ABP的面积S最大为20.
解析:
(1)过C点作CE⊥AB于E,
 在△BEC中,CE=
在△BEC中,CE=![]() =4,∴sinB=
=4,∴sinB=![]() .
.
由题意,当x∈(0,5]时,过P点作PF⊥AB于F,
∴PF=xsinB=![]() x,∴S=
x,∴S=![]() ×10×
×10×![]() x=4x,
x=4x,
当x∈(5,9]时,∴S=![]() ×10×4=20.
×10×4=20.
当x∈(9,14]时,AP=14-x,PF=AP·sinA=![]() ,
,
∴S=![]() ×10×(14-x) ×
×10×(14-x) ×![]() =56-4x.综上可知,函数S=f(x)=
=56-4x.综上可知,函数S=f(x)=
(2)由(1)知,当x∈(0,5]时,f(x)=4x为增函数,
所以,当x=5时,取得最大值20.
当x∈(5,9]时,f(x)=20,最大值为20.
当x∈(9,14]时,f(x)=56-4x为减函数,无最大值.
综上可知:当P点在CD上时,△ABP的面积S最大为20.

练习册系列答案
相关题目
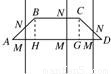
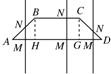 等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线MN⊥AD交AD于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为x的函数,并写出函数的定义域.
等腰梯形ABCD的两底分别为AD=2a,BC=a,∠BAD=45°,作直线MN⊥AD交AD于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为x的函数,并写出函数的定义域.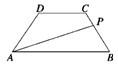 等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S
等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S 如图所示,等腰梯形ABCD的两底分别为AD=2,BC=1,∠BAD=45°,直线MN⊥AD交于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧面积y表示为x的函数,并写出函数的定义域.
如图所示,等腰梯形ABCD的两底分别为AD=2,BC=1,∠BAD=45°,直线MN⊥AD交于M,交折线ABCD于N,记AM=x,试将梯形ABCD位于直线MN左侧面积y表示为x的函数,并写出函数的定义域.