题目内容
2.各项均为正数的等比数列{an},a1=1,a2a4=16,数列{bn}的前n项和为Sn,且Sn=$\frac{3{n}^{2}+n}{2}$(n∈N+).(1)求数列{an},{bn}的通项公式;
(2)cn=anbn(n∈N+),求数列{cn}的前n项和Tn;
(3)若dn=an+(-1)nbn,设数列{dn}的前n项和为Un,求Un.
分析 (1)运用等比数列的通项公式可得an=2n-1:再由数列的通项和求和的关系,可得n>1时,an=Sn-Sn-1,注意检验n=1的情况;
(2)求得cn=anbn=(3n-1)•2n-1,运用错位相减法,结合等比数列的求和公式,即可得到;
(3)dn=an+(-1)nbn=2n-1+(-1)n•(3n-1),讨论n为偶数和奇数,运用分组求和,结合等比数列和等差数列的求和公式,计算即可得到.
解答 解:(1)设等比数列{an}的公比为q,
由a1=1,a2a4=16,可得q4=16,解得q=2,(-2舍去),
即有an=2n-1:
由Sn=$\frac{3{n}^{2}+n}{2}$(n∈N+),可得a1=S1=2,
n>1时,an=Sn-Sn-1=$\frac{3{n}^{2}+n}{2}$-$\frac{3(n-1)^{2}+(n-1)}{2}$
=3n-1,对n=1也成立,
则bn=3n-1;
(2)cn=anbn=(3n-1)•2n-1,
Tn=2+5•2+8•22+…+(3n-1)•2n-1,
2Tn=2•2+5•22+8•23+…+(3n-1)•2n,
两式相减可得,-Tn=2+3(2+22+…+2n-1)-(3n-1)•2n,
=2+3•$\frac{2(1-{2}^{n-1})}{1-2}$-(3n-1)•2n,
化简可得Tn=4+(3n-4)•2n;
(3)dn=an+(-1)nbn=2n-1+(-1)n•(3n-1),
当n为偶数时,Un=(1+2+…+2n-1)+(-2+5)+(-8+11)+…+(-3n+4+3n-1)
=$\frac{1-{2}^{n}}{1-2}$+$\frac{3n}{2}$=$\frac{3}{2}$n+2n-1;
当n为奇数时,Un=Un-1+dn=$\frac{3}{2}$(n-1)+2n-1-1+2n-1-(3n-1)
=2n-$\frac{3n+3}{2}$.
即有Un=$\left\{\begin{array}{l}{{2}^{n}-\frac{3n+3}{2},n为奇数}\\{{2}^{n}+\frac{3n-2}{2},n为偶数}\end{array}\right.$.
点评 本题考查等差数列和等比数列的通项公式及求和公式的运用,考查数列的求和方法:错位相减法和分组求和,考查分类讨论的思想方法,属于中档题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | -4 | B. | 4 | C. | -6或4 | D. | 6或4 |
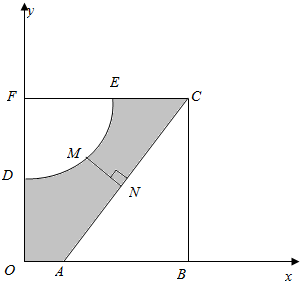 如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF=$\frac{9}{4}$km,FE=3km,EC=$\frac{3}{2}$km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=$\frac{x+b}{x+a}$(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.
如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF=$\frac{9}{4}$km,FE=3km,EC=$\frac{3}{2}$km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=$\frac{x+b}{x+a}$(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.