题目内容

13．对于矩形ABCD，若AB=3，BC=4，以边AB为轴旋转形成圆柱，那么绕圆柱一周的绳子由C点到D点最短多长？

分析 要求这根绳子的最短长度，需将圆柱的侧面展开，进而根据勾股定理得出结果．

解答 解：如图，将圆柱体展开，得到矩形CDD′C′，连接CD′，则线段CD′的长即为绳子最短的长度．
在△CDD′中，DD′=8π，CD=3，
由勾股定理，得CD′=$\sqrt{64{π}^{2}+9}$，
即这根绳子的最短长度为$\sqrt{64{π}^{2}+9}$．

点评 本题考查了平面展开-最短路径问题及圆柱体的侧面展开图，掌握圆柱体的侧面展开图是一个矩形，其中矩形的长是圆柱的底面周长，宽是圆柱的高是解题的关键．

练习册系列答案
相关题目
3．某地气中出现污染，须喷洒一定量的去污剂进行处理．据测算，每喷洒1个单位的去污剂，空气中释放的浓度y（单位：毫克/立方米）随着时间x（单位：天）变化的函数关系式近似为$y=\left\{\begin{array}{l}\frac{16}{8-x}-1，0≤x≤4\\ 5-\frac{1}{2}x，4＜x≤10\end{array}\right.$，若多次喷洒，则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和．由实验知，当空气中去污剂的浓度不低于4（毫克/立方米）时，它才能起到去污作用．
（Ⅰ）若一次喷洒4个单位的去污剂，则去污时间可达几天？
（Ⅱ）若第一次喷洒2个单位的去污剂，6天后再喷洒a（1≤a≤4）个单位的去污剂，要使接下来的4天中能够持续有效去污，试求a的最小值（精确到0.1，参考数据：$\sqrt{2}$取1.4）．
4．已知集合U={1，2，3，4，5，6，7}，A={x∈R|数轴上x到3的距离等于1，或x到6的距离等于1}，B={x∈Z|$\frac{2x-11}{2-x}≥0$}，求（∁UA）∪（∁UB）．
1．设不等式组$\left\{\begin{array}{l}{y≥0}\\{y≤4}\\{kx-y≥0}\\{kx-y-4k≤0}\end{array}\right.$表示的平面区域为W
（1）若k=2，M（x，y）为区域W内的动点，求x+2y的最大值；
（2）区域W内部的整点的个数有多少？（整点是指横、纵坐标都是整数的点）．
8．设l，m，n表示三条直线，α，β，γ表示三个平面，给出下列六个命题：
  ①若1⊥α，m⊥α，则l∥m；
  ②若l⊥α，m?β，l∥m，则α⊥β；
  ③若l⊥α，m?β，l⊥m，则α∥β；
  ④若m?β，n是l在β内的射影，m⊥l，则m⊥n；
  ⑤若m?α，m∥n，则n∥α；
  ⑥若α⊥γ，β⊥γ，则α∥β．
  其中正确命题的个数是（　　）
A．1B．3C．4D．5
18．某市城区实行三级阶梯水价（阶梯水价就是分段累计计费），第一阶梯水价为每户每月12吨以下（含12吨）部分，价格为1.60元/吨；第二阶梯水价为每户每月12-20 吨（含20吨）部分，价格为2.40元/吨；第三阶梯水量为每户每月20吨以上部分，价格为3.20元/吨，
（1）写出某用户每月用水量x吨与其水费y元之间的函数关系式；
（2）某用户5月份的水费是31.2元，该用户这个月用水多少吨？
5．圆C：x2+y2-6x-8y+23=0的半径为（　　）
A．$\sqrt{2}$B．2C．2$\sqrt{2}$D．4
2．各项均为正数的等比数列{an}，a1=1，a2a4=16，数列{bn}的前n项和为Sn，且Sn=$\frac{3{n}^{2}+n}{2}$（n∈N+）．
（1）求数列{an}，{bn}的通项公式；
（2）cn=anbn（n∈N+），求数列{cn}的前n项和Tn；
（3）若dn=an+（-1）nbn，设数列{dn}的前n项和为Un，求Un．
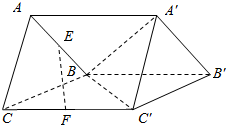3．如图，三棱柱ABC-A′B′C′，E，F分别是AB，CC′的中点，过EF作一个平面和面A′BC′相交，并找到交线，写出作法．（注意：交线必须是由两个确定的点的连线）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网