Question

直线l：y=m（m为实常数）与曲线E：y=|lnx|的两个交点A、B的横坐标分别为x₁、x₂，且x₁＜x₂，曲线E在点A、B处的切线PA、PB与y轴分别交于点M、N，有下面4个结论：
①|

MN

|=2；
②三角形PAB可能为等腰三角形；
③若直线l与y轴的交点为Q，则|PQ|=1；
④是函数g（x）=x²+lnx的零点时，|

AO

|（O为坐标原点）取得最小值．
其中正确结论有

 

．（写出所有正确结论的序号）

Answer 1

考点：命题的真假判断与应用

专题：作图题,函数的性质及应用,导数的综合应用

分析：①画出y=m和y=|lnx|的图象，求出切线的斜率，求出交点的坐标M，N，即可得到MN的长，即可判断①；
②通过图象观察分析，两切线垂直，即可判断②；
③求出P的坐标，再求PQ长，即可判断③；
④由零点的定义，求出AO的长，运用函数的性质，即可判断④．

解答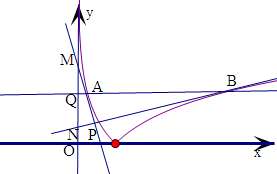： 解：对于①，作出函数的图象，由|lnx₁|=|lnx₂|，可得，-lnx₁=lnx₂，
所以x₁x₂=1，且0＜x₁＜1，x₂＞1，故A（x₁，-lnx₁）B（x₂，lnx₂），
在A点处的切线斜率为-

1

x1

，在B点处的切线斜率为：

1

x2

，
则设M（0，s），N（0，n），
则有

s+lnx1

-x1

=-

1

x1

，解得，s=1-lnx₁，
由

n-lnx2

-x2

=

1

x2

，解得，n=lnx₂-1，
则有|MN|=1-lnx₁-（lnx₂-1）=2-ln（x₁x₂）=2，故①正确；
对于②，若△PAB为等腰三角形，即PA=PB，或PA=AB，或PB=AB，
若PA=PB，则P在AB的中垂线上，不可能；若PA=AB，易得P的横坐标小于1，不成立；
若PB=AB，则由于-

1

x1

•

1

x2

=-1，即有PA⊥BP，则不成立，故②错误；
对于③，Q（0，m），由y+lnx₁=1-

1

x1

x和y-lnx₂=

x

x2

-1，x₁x₂=1，
解得交点P（

2x1

1+x12

，1-lnx₁-

2

1+x12

），由于m=lnx₂=-lnx₁，
则有|PQ|=

( 2x1 1+x12 )2+( x12-1 1+x12 )2

=1．故③正确；
对于④，当x₁是函数g（x）=x²+lnx的零点时，即有x₁²+lnx₁=0，
|

AO

|=

x12+(lnx1)2

=

x14+x12

，由于0＜x₁＜1，则取不到最小值，故④错误．
故答案为：①③．

点评：本题考查导数的几何意义，着重考查曲线在该点处的切线的斜率，两点的距离和点到直线的距离公式及函数的最值的求法，考查转化思想与分析运算、判断求解能力，属于难题．