题目内容
设函数![]() 其中实数
其中实数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(2)当函数![]() 与
与![]() 的图象只有一个公共点且
的图象只有一个公共点且![]() 存在最小值时,记
存在最小值时,记![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值域;
的值域;
(3)若![]() 与
与![]() 在区间
在区间![]() 内均为增函数,求
内均为增函数,求![]() 的取值范围.
的取值范围.
解:(Ⅰ)若![]() ,
,![]()
![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
, ![]()
![]() 的增区间为
的增区间为![]() 和
和![]() .
.
(Ⅱ)由题意知 ![]() ,
,
即![]() 恰有一根(含重根).
恰有一根(含重根).
![]()
![]() ≤
≤![]() ,即
,即![]() ≤
≤![]() ≤
≤![]() ,
,
又![]() ,
,
![]()
![]() .
.
当![]() 时,
时,![]() 才存在最小值,
才存在最小值,
![]()
![]() .
.
![]()
![]() ,
,
![]()
![]() .
.
![]()
![]() 的值域为
的值域为![]() .
.
(Ⅲ)当![]() 时,
时,![]() 在
在![]() 和
和![]() 内是增函数,
内是增函数,![]() 在
在![]() 内是增函数.
内是增函数.
由题意得![]() ,解得
,解得![]() ≥
≥![]() ;
;
当![]() 时,
时,![]() 在
在![]() 和
和![]() 内是增函数,
内是增函数,![]() 在
在![]() 内是增函数.
内是增函数.
由题意得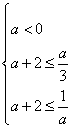 ,解得
,解得![]() ≤
≤![]() ;
;
综上可知,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
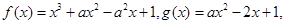 其中实数
其中实数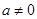 .
.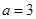 时,求函数
时,求函数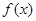 的单调区间;
的单调区间;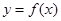 与
与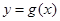 的图象只有一个公共点且
的图象只有一个公共点且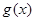 存在最小值时,
存在最小值时,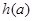 ,求函数
,求函数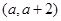 内均为增函数,求实数
内均为增函数,求实数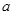 的取值范围.
的取值范围.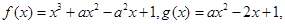 其中实数
其中实数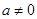 .
.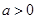 ,求函数
,求函数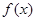 的单调区间;
的单调区间;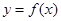 与
与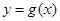 的图象只有一个公共点且
的图象只有一个公共点且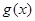 存在最小值时,记
存在最小值时,记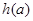 ,求
,求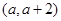 内均为增函数,求
内均为增函数,求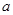 的取值范围.
的取值范围.