题目内容
(本题满分16分)
设函数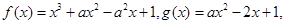 其中实数
其中实数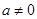 .
.
(1)当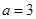 时,求函数
时,求函数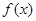 的单调区间;
的单调区间;
(2)当函数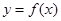 与
与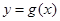 的图象只有一个公共点且
的图象只有一个公共点且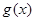 存在最小值时,
存在最小值时,
记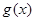 的最小值为
的最小值为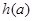 ,求函数
,求函数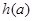 的值域;
的值域;
(3)若函数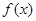 与
与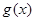 在区间
在区间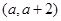 内均为增函数,求实数
内均为增函数,求实数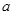 的取值范围.
的取值范围.
【答案】
(1)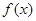 的单调增区间为
的单调增区间为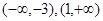
单调减区间为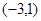
(2)
(3)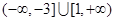
【解析】解:(1) 当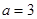 时,
时,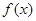 =
=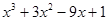
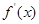 =
=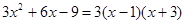 …………………………2分
…………………………2分
由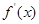 >0得
>0得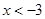 或
或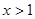 由
由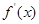 <0,得
<0,得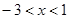
∴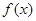 的单调增区间为
的单调增区间为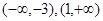
单调减区间为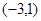 ……………………………………5分
……………………………………5分
(2)由题意知 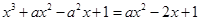 ,
,
即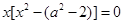 恰有一根(含重根).
恰有一根(含重根).
∴ 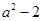 ≤
≤ ,即
,即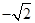 ≤
≤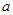 ≤
≤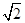 ,又
,又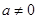 ,∴
,∴ 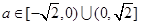 .
.
当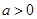 时,
时,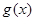 才存在最小值,
才存在最小值,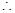
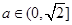 ………………………8分
………………………8分
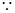
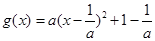 ,
,
∴ 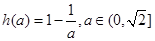 . ∴
. ∴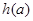 的值域为
的值域为 …………10分
…………10分
(3)当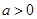 时,
时,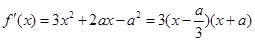 ,
,
∴ 当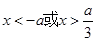 时,
时,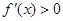 ;当
;当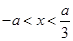 时,
时,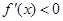 ,
,
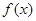 在
在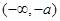 和
和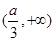 内是增函数,
内是增函数,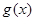 在
在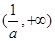 内是增函数.
内是增函数.
由题意得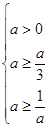 ,解得
,解得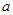 ≥
≥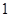 ……………………………………13分
……………………………………13分
当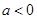 时,
时,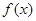 在
在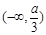 和
和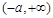 内是增函数,
内是增函数,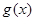 在
在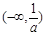 内是增函数.
内是增函数.
由题意得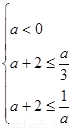 ,解得
,解得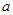 ≤
≤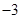 ……………………………………15分
……………………………………15分
综上可知,实数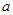 的取值范围为
的取值范围为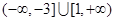 ………………………16分
………………………16分

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在