题目内容
已知数列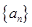 的前n项和为
的前n项和为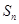 ,点
,点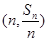 在直线
在直线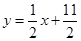 上.数列{bn}满足
上.数列{bn}满足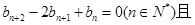
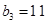 ,前9项和为153.
,前9项和为153.
(Ⅰ)求数列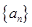 、
、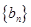 的通项公式;
的通项公式;
(Ⅱ)设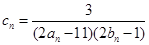 ,数列
,数列 的前n和为
的前n和为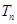 ,求使不等式
,求使不等式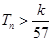 对一切
对一切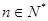 都成立的最大正整数k的值.
都成立的最大正整数k的值.
(1) , bn=b3+3(n﹣3)=3n+2;
, bn=b3+3(n﹣3)=3n+2;
(2)
解析试题分析:解:(1)∵点 在直线
在直线 上,
上,
∴ ∴Sn=
∴Sn= ∴n≥2时,an=Sn﹣Sn﹣1=n+5,
∴n≥2时,an=Sn﹣Sn﹣1=n+5,
n=1时,a1=6也符合
∴an=n+5;∵bn+2﹣2bn+1+bn=0,∴bn+2﹣bn+1=bn+1﹣bn,
∴数列{bn}是等差数列∵其前9项和为153.
∴b5=17∵b3=11,∴公差d= =3
=3
∴bn=b3+3(n﹣3)=3n+2;
(2) =
= (
( )
)
∴Tn= (1﹣
(1﹣ +
+ ﹣
﹣ +…+
+…+ )=
)= =
= .
.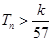
解得

考点:等差数列和数列的求和
点评:主要是考查了等差数列和裂项法求和的运用,属于中档题。

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
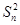 -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.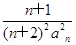 ,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn< 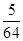 .
.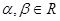 且
且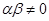 ,数列
,数列 满足
满足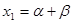 ,
,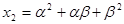 ,
,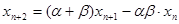 (
(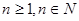 ),令
),令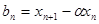 ,
,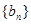 是等比数列;
是等比数列;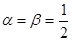 ,求
,求 项和
项和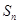 .
. 的各项均为正数,其前
的各项均为正数,其前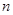 项和为
项和为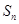 ,且
,且 .
.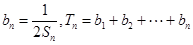 ,求证:
,求证: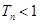 ;
;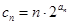 ,
,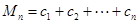 ,求
,求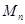 .
.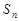 为数列
为数列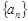 的前
的前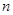 项和,且
项和,且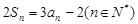 .
.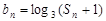 ,求数列
,求数列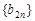 的前n项和
的前n项和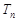 .
. 中,
中,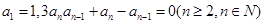
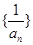 是否为等差数列;
是否为等差数列;
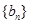 满足
满足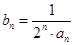 ,求数列
,求数列 ;
;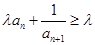 ,对任意n ≥2的整数恒成立,求实数
,对任意n ≥2的整数恒成立,求实数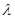 的取值范围.
的取值范围.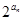 }的前n项和Sn.
}的前n项和Sn.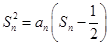 .
.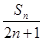 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn. 满足:
满足: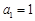 ,
,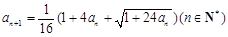 。
。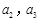 ;
; 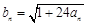 ,求数列
,求数列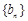 的通项公式;
的通项公式;