题目内容
15.已知函数f(x)=2sinx•cosx+2cos2x-1,(1)求函数f(x)的单调递增区间.
(2)求函数f(x)的最大值及f(x)取最大值时x的集合.
分析 (1)由条件利用两角和差的正弦公式,化简函数的解析式,再利用正弦函数的单调性求得f(x)的单调递增区间.
(2)根据函数f(x)的解析式,再根据正弦函数的最值,求得函数f(x)的最大值及f(x)取最大值时x的集合.
解答 解:(1)函数f(x)=2sinx•cosx+2cos2x-1=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{3π}{8}$≤x≤kπ+$\frac{π}{8}$,可得函数的单调增区间为[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z.
(2)由f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),可得当2x+$\frac{π}{4}$=2kπ+$\frac{π}{2}$,k∈Z时,函数f(x)取得最大值为$\sqrt{2}$,
此时,x取值的集合为{x|x=kπ+$\frac{π}{8}$,k∈Z}.
点评 本题主要考查两角和差的正弦公式,正弦函数的单调性和最值,属于基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
5.函数y=sin(ωx+φ)的部分图象如图,则f($\frac{π}{2}$)=( )


| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
10. 如图所示韦恩图I、Ⅱ、Ⅲ、Ⅳ区中,Ⅳ区阴影可由( )表示.
如图所示韦恩图I、Ⅱ、Ⅲ、Ⅳ区中,Ⅳ区阴影可由( )表示.
 如图所示韦恩图I、Ⅱ、Ⅲ、Ⅳ区中,Ⅳ区阴影可由( )表示.
如图所示韦恩图I、Ⅱ、Ⅲ、Ⅳ区中,Ⅳ区阴影可由( )表示.| A. | A∩B | B. | ∁AB | C. | ∁BA | D. | ∁∪(A∪B) |
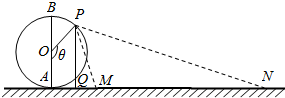 如图,摩天轮的半径OA为50m,它的最低点A距地面的高度忽略不计.地面上有一长度为240m的景观带MN,它与摩天轮在同一竖直平面内,且AM=60m.点P从最低点A处按逆时针方向转动到最高点B处,记∠AOP=θ,θ∈(0,π).
如图,摩天轮的半径OA为50m,它的最低点A距地面的高度忽略不计.地面上有一长度为240m的景观带MN,它与摩天轮在同一竖直平面内,且AM=60m.点P从最低点A处按逆时针方向转动到最高点B处,记∠AOP=θ,θ∈(0,π).