题目内容
已知定点 ,
, ,动点
,动点 到定点
到定点 距离与到定点
距离与到定点 的距离的比值是
的距离的比值是 .
.
(Ⅰ)求动点 的轨迹方程,并说明方程表示的曲线;
的轨迹方程,并说明方程表示的曲线;
(Ⅱ)当 时,记动点
时,记动点 的轨迹为曲线
的轨迹为曲线 .
.
①若 是圆
是圆 上任意一点,过
上任意一点,过 作曲线
作曲线 的切线,切点是
的切线,切点是 ,求
,求 的取值范围;
的取值范围;
②已知 ,
, 是曲线
是曲线 上不同的两点,对于定点
上不同的两点,对于定点 ,有
,有 .试问无论
.试问无论 ,
, 两点的位置怎样,直线
两点的位置怎样,直线 能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
【答案】
(Ⅰ)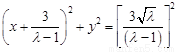 ,
,
方程表示的曲线是以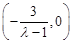 为圆心,
为圆心,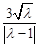 为半径的圆.
为半径的圆.
(Ⅱ)当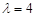 时,曲线
时,曲线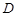 的方程是
的方程是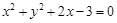 ,曲线
,曲线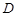 表示圆,圆心是
表示圆,圆心是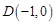 ,半径是
,半径是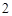 .
.
①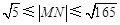 .
.
②动直线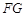 与定圆
与定圆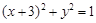 相切.
相切.
【解析】
试题分析:(Ⅰ)设动点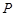 的坐标为
的坐标为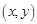 ,则由
,则由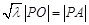 ,得
,得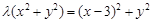 ,
,
整理得: 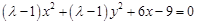 .
.
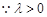 ,
,
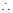 当
当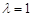 时,则方程可化为:
时,则方程可化为: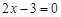 ,故方程表示的曲线是线段
,故方程表示的曲线是线段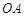 的垂直平分线;
的垂直平分线;
当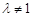 时,则方程可化为
时,则方程可化为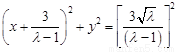 ,
,
即方程表示的曲线是以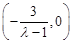 为圆心,
为圆心,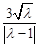 为半径的圆.
5分
为半径的圆.
5分
(Ⅱ)当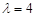 时,曲线
时,曲线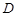 的方程是
的方程是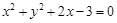 ,
,
故曲线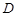 表示圆,圆心是
表示圆,圆心是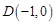 ,半径是
,半径是 .
.
①由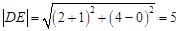 ,及
,及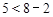 有:
有:
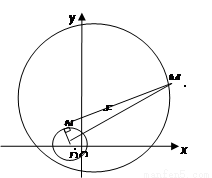
两圆内含,且圆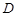 在圆
在圆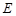 内部.如图所示,由
内部.如图所示,由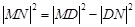 有:
有: 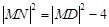 ,故求
,故求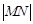 的取值范围就是求
的取值范围就是求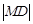 的取值范围.而
的取值范围.而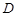 是定点,
是定点,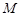 是圆上的动点,故过
是圆上的动点,故过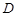 作圆
作圆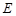 的直径,得
的直径,得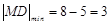 ,
,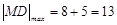 ,故
,故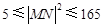 ,
,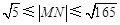 .
9分
.
9分
②设点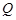 到直线
到直线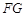 的距离为
的距离为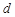 ,
,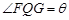 ,
,
则由面积相等得到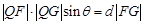 ,且圆的半径
,且圆的半径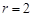 .
.
即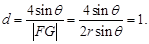 于是顶点
于是顶点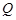 到动直线
到动直线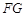 的距离为定值,
的距离为定值,
即动直线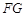 与定圆
与定圆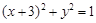 相切.
相切.
考点:圆的方程,圆与圆的位置关系,直线与圆的位置关系。
点评:难题,本题确定轨迹方程,利用了“直接法”,对于参数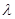 的讨论,易出现遗漏现象。本题确定点到直线的距离,转化成面积计算,不易想到。
的讨论,易出现遗漏现象。本题确定点到直线的距离,转化成面积计算,不易想到。

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 到定点
到定点 的距离与它到定直线
的距离与它到定直线 的距离相等
的距离相等 的方程
的方程 作直线
作直线 交
交 于
于 两点(
两点( 在第一象限),若
在第一象限),若 ,求直线
,求直线 ,过点
,过点 交抛物线
交抛物线 于
于 两点,使得
两点,使得 ?若存在,求出点
?若存在,求出点