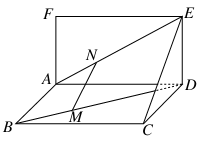
题目内容
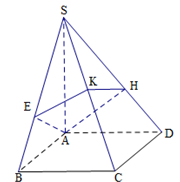
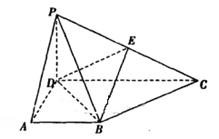
如图,四棱锥 的底面是正方形,侧棱
的底面是正方形,侧棱 底面
底面 ,过
,过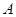 作
作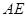 垂直
垂直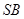 交
交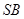 于
于 点,作
点,作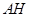 垂直
垂直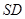 交
交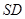 于
于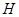 点,平面
点,平面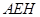 交
交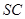 于
于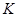 点,且
点,且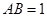 ,
,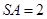 .
.
(1)设点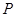 是
是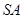 上任一点,试求
上任一点,试求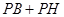 的最小值;
的最小值;
(2)求证: 、
、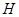 在以
在以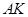 为直径的圆上;
为直径的圆上;
(3)求平面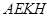 与平面
与平面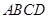 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(1)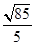 ;(2)详见解析;(3)
;(2)详见解析;(3)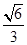 .
.
解析试题分析:(1)将侧面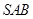 和侧面
和侧面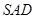 沿着
沿着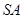 展开至同一平面上,利用
展开至同一平面上,利用 、
、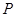 、
、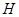 三点共线结合余弦定理求出
三点共线结合余弦定理求出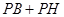 的最小值,即线段
的最小值,即线段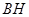 的长度;(2)证
的长度;(2)证 平面
平面 ,从而得到
,从而得到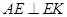 ,同理得到
,同理得到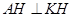 ,进而证明
,进而证明 、
、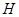 在以
在以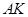 为直径的圆上;(3)方法一是建立以点
为直径的圆上;(3)方法一是建立以点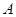 为坐标原点,分别以
为坐标原点,分别以 、
、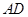 、
、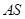 所在的直线为
所在的直线为 、
、 、
、 轴的空间直角坐标系,利用空间向量法求平面
轴的空间直角坐标系,利用空间向量法求平面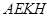 与平面
与平面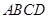 所成的锐二面角的余弦值;方法二是延长
所成的锐二面角的余弦值;方法二是延长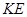 与
与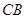 使得它们相交,找出二面角的棱,然后利用三垂线法找出平面
使得它们相交,找出二面角的棱,然后利用三垂线法找出平面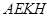 与平面
与平面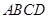 所成的锐二面角的平面角,利用直角三角函数来求相应角的余弦值.
所成的锐二面角的平面角,利用直角三角函数来求相应角的余弦值.
试题解析:(1)将侧面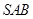 绕侧棱
绕侧棱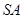 旋转到与侧面
旋转到与侧面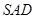 在同一平面内,如下图示,
在同一平面内,如下图示,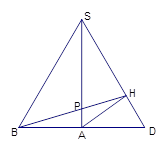
则当 、
、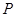 、
、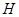 三点共线时,
三点共线时,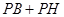 取最小值,这时,
取最小值,这时,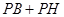 的最小值即线段
的最小值即线段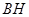 的长,
的长,
设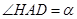 ,则
,则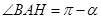 ,
,
在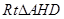 中,
中,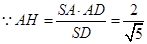 ,
, ,
,
在三角形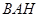 中,有余弦定理得:
中,有余弦定理得: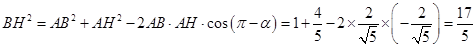 ,
,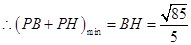 ,
,
(2)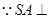 底面
底面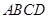 ,
,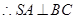 ,又
,又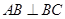
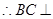 平面
平面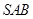 ,又
,又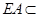 平面
平面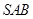 ,
,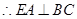 ,
,
又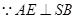 ,
,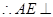 平面
平面 ,
,
又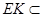 平面
平面 ,
,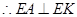 ,
,
同理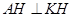 ,
,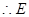 、
、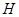 在以
在以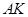 为直径的圆上;
为直径的圆上;
(3)方法一:如图,以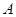 为原点,分别以
为原点,分别以 、
、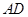 、
、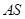 所在的直线为
所在的直线为
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目

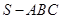 中,
中,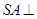 底面
底面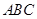 ,点
,点 为以
为以 为直径的圆上任意一动点,且
为直径的圆上任意一动点,且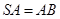 ,点
,点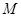 是
是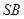 的中点,
的中点,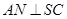 且交
且交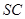 于点
于点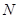 .
. 面
面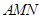 ;
;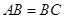 时,求二面角
时,求二面角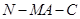 的余弦值.
的余弦值.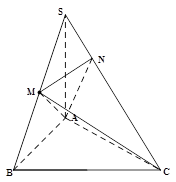
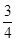 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4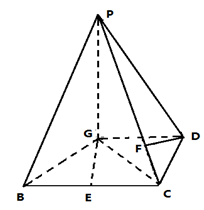
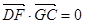 ,
,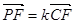 ,求
,求 的值.
的值.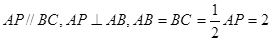 ,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP
,D是AP的中点,E,G分别为PC,CB的中点,将三角形PCD沿CD折起,使得PD垂直平面ABCD.(1)若F是PD的中点,求证:AP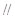 平面EFG;(2)当二面角G-EF-D的大小为
平面EFG;(2)当二面角G-EF-D的大小为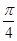 时,求FG与平面PBC所成角的余弦值.
时,求FG与平面PBC所成角的余弦值.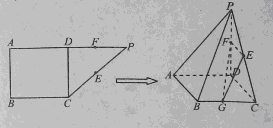
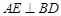 于
于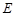 ,延长AE交BC于F,将
,延长AE交BC于F,将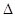 ABD沿BD折起,使平面ABD
ABD沿BD折起,使平面ABD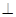 平面BCD,如图2所示.
平面BCD,如图2所示.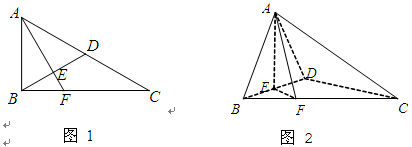
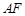 上是否存在点
上是否存在点 使得
使得 平面
平面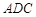 ?若存在,请指明点
?若存在,请指明点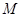 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由. 底面ABCD,PD
底面ABCD,PD ,
,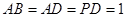 ,
, .
.
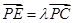 ,试确定
,试确定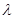 的值,使得二面角E-BD-P的余弦值为
的值,使得二面角E-BD-P的余弦值为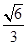 .
.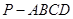 中,
中,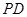
 底面
底面 ,且底面
,且底面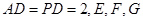 分别为
分别为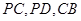 的中点.
的中点.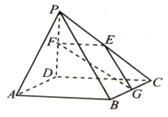
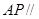 平面
平面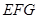 ;
;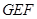 和平面
和平面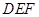 的夹角.
的夹角. 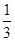 BD,AN=
BD,AN=