题目内容
设| a |
| b |
| a |
| b |
| 3 |
| 8 |
（Ⅰ）求?；
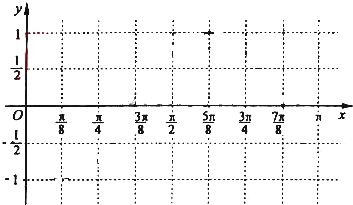
（Ⅱ）在给出的直角坐标系中用五点作图法画出函数y=f（x）在区间[0，π]上的图象；
（Ⅲ）根据画出的图象写出函数y=f（x）在[0，π]上的单调区间和最值．
分析：（Ⅰ）由f(x)=
•
=sin2xcos?+cos2xsin?=sin（2x+?）可得sin(2×
π+?)=0，结合0＜?＜π，可求
（Ⅱ）列表，画出函数的图象
（Ⅲ）结合函数的图象可求函数的单调区间及函数的最值
| a |
| b |
| 3 |
| 8 |
（Ⅱ）列表，画出函数的图象
（Ⅲ）结合函数的图象可求函数的单调区间及函数的最值
解答：解：（Ⅰ）∵f(x)=
•
=sin2xcos?+cos2xsin?=sin（2x+?）…（2分）
由题可知：sin(2×
π+?)=0，…（3分）
∴
π+?=kπ(k∈Z)，…（4分）
∵0＜?＜π，
∴?=
…（5分）
（Ⅱ）∵f（x）=sin（2x+
）
列表因为x∈[0，π]，所以2x+
∈[
，
]
…（9分）
（Ⅲ）单调增区间：[0，
]，[
，π]…（10分）
单调减区间：[
，
π]…（11分）
函数的最大值是：1，最小值-1
| a |
| b |
由题可知：sin(2×
| 3 |
| 8 |
∴
| 3 |
| 4 |
∵0＜?＜π，
∴?=
| π |
| 4 |
（Ⅱ）∵f（x）=sin（2x+
| π |
| 4 |
列表因为x∈[0，π]，所以2x+
| π |
| 4 |
| π |
| 4 |
| 9π |
| 4 |
2x+
|
|
|
π |
|
2π |
| ||||||||||
| x | 0 |
|
|
|
|
π | ||||||||||
| f（x） |
|
1 | 0 | -1 | 0 |
|
…（9分）（Ⅲ）单调增区间：[0，
| π |
| 8 |
| 5π |
| 8 |
单调减区间：[
| π |
| 8 |
| 5 |
| 8 |
函数的最大值是：1，最小值-1
点评：此题考查了函正弦函数性质的应用，函数单调区间的求解，涉及的知识有：平面向量的数量积运算，两角和与差的正弦函数公式，辅助角公式的应用，以及正弦函数的单调性，其中利用三角函数的恒等变形把函数解析式化为一个角的正弦函数是解本题的关键．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
sin2x,cos2x),b=(sin2x,sin2x)，若函数f(x)=a·b+t(t∈R),
,
］时，函数f(x)的最大值为3,求函数f(x)的最小值,并求此时的x值.