题目内容
已知圆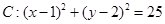 ,直线
,直线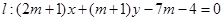 ,
,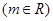 。
。
(1)证明:不论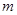 取什么实数,直线
取什么实数,直线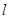 与圆恒交于两点;
与圆恒交于两点;
(2)求直线被圆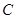 截得的弦长最小时
截得的弦长最小时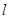 的方程.
的方程.
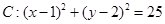 ,直线
,直线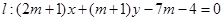 ,
,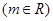 。
。(1)证明:不论
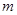 取什么实数,直线
取什么实数,直线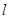 与圆恒交于两点;
与圆恒交于两点;(2)求直线被圆
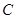 截得的弦长最小时
截得的弦长最小时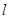 的方程.
的方程.(1)见解析;(2)2x-y-5=0
试题分析:(1)直线与圆恒有交点,说明直线恒过的定点在圆内,所以关键是找到直线恒过的定点,要把直线
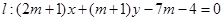 改写成
改写成 的形式,然后令m的系数为零即可.(2)圆的弦长最小值的计算,常用两种方法:第一、通过弦长的计算再求最小值;第二、通过计算最长的弦心距来研究最短的弦.
的形式,然后令m的系数为零即可.(2)圆的弦长最小值的计算,常用两种方法:第一、通过弦长的计算再求最小值;第二、通过计算最长的弦心距来研究最短的弦.试题解析:(1)证法1:
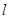 的方程
的方程 ,
,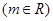
 即
即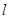 恒过定点
恒过定点
圆心坐标为
 ,半径
,半径 ,
, ,
,∴点
 在圆
在圆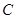 内,从而直线
内,从而直线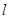 恒与圆
恒与圆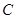 相交于两点。
相交于两点。证法2:圆心到直线
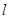 的距离
的距离 ,
,
 ,所以直线
,所以直线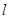 恒与圆
恒与圆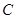 相交于两点。
相交于两点。(2)弦长最小时,
 ,
,
 ,
, ,
,
代入
 ,
,得
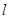 的方程为
的方程为 。
。
练习册系列答案
相关题目
 的圆心在点
的圆心在点 ,点
,点 ,求;
,求; 的圆的切线方程;
的圆的切线方程; 点是坐标原点,连结
点是坐标原点,连结 ,
, ,求
,求 的面积
的面积 .
. 有公共点的概率.
有公共点的概率.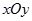 中,已知圆
中,已知圆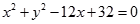 的圆心为
的圆心为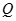 ,过点
,过点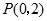 且斜率为
且斜率为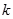 的直线与圆
的直线与圆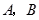 .
. :
: 被圆
被圆
 截得的弦
截得的弦 的长是 .
的长是 . 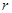 是常数,如果
是常数,如果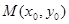 是圆
是圆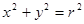 外的一点,那么直线
外的一点,那么直线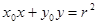 与圆
与圆 上有且仅有两个点到直线
上有且仅有两个点到直线 的距离为
的距离为 ,则半径
,则半径 的取值范围是 .
的取值范围是 . ,
, ,直线
,直线 :
: ,圆
,圆 :
: .若圆
.若圆 又与直线
又与直线 的取值范围是________.
的取值范围是________. 相切, 且与直线
相切, 且与直线 垂直, 则
垂直, 则 ( )
( )
