Question

【题目】已知圆上一动点，过点作轴，垂足为点，中点为．

（1）当在圆上运动时，求点的轨迹的方程；

（Ⅱ）过点的直线与交于两点，当时，求线段的垂直平分线方程．

Answer 1

【答案】(1)；(2)或．

【解析】分析：（1）要求点的轨迹的方程，可设点的坐标为，由条件过点作轴，垂足为点，中点为，可写出点A的坐标。因为点在圆上，故可将点的坐标代入圆的方程，可得点的轨迹。

(2)要线段的垂直平分线方程，应先求直线的方程，所以应设直线的方程，根据弦长求直线的方程。因为直线的斜率是否存在不确定，为了避免讨论，可设直线方程为：，并与轨迹的方程联立可得，由根与系数的关系可得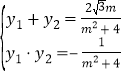，由弦长公式可得，可解得。分情况讨论，求线段的中点，直线的斜率，进而可求线段的垂直平分线方程。

详解：（1）设，则

将代入圆方程得：点的轨迹

（注：学生不写也不扣分）

（2）由题意可设直线方程为：，

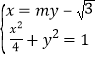由得：

所以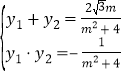

所以．

当时，中点纵坐标，代入得：

中点横坐标，斜率为

故的垂直平分线方程为：

当时，同理可得的垂直平分线方程为：

所以的垂直平分线方程为：或．