题目内容
【题目】已知![]() 为椭圆
为椭圆![]() 上两点,过点
上两点,过点![]() 且斜率为
且斜率为![]() 的两条直线与椭圆
的两条直线与椭圆![]() 的交点分别为
的交点分别为![]() .
.
(Ⅰ)求椭圆![]() 的方程及离心率;
的方程及离心率;
(Ⅱ)若四边形![]() 为平行四边形,求
为平行四边形,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ,离心率
,离心率![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由题列a,b方程组,即可求解椭圆方程,再由a,b,c关系,求解离心率;(Ⅱ)设直线![]() 的方程为
的方程为![]() ,与椭圆联立消去y,得x的方程,求点B坐标,同理求点C坐标,进而得
,与椭圆联立消去y,得x的方程,求点B坐标,同理求点C坐标,进而得![]() 再由
再由![]() ,得k方程求解即可
,得k方程求解即可
(I)由题意得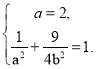 解得
解得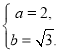
所以椭圆![]() 的方程为
的方程为![]() .
.
又![]() ,
,
所以离心率![]() .
.
(II)设直线![]() 的方程为
的方程为![]() ,
,
由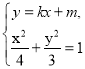 消去
消去![]() ,整理得
,整理得![]() .
.
当![]() 时,设
时,设![]() ,
,
则![]() ,即
,即![]() .
.
将![]() 代入
代入![]() ,整理得
,整理得![]() ,所以
,所以![]() .
.
所以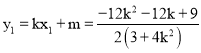 .所以
.所以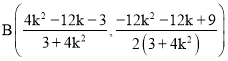 .
.
同理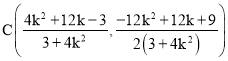 .
.
所以直线![]() 的斜率
的斜率![]() .
.
又直线![]() 的斜率
的斜率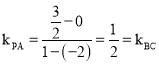 ,所以
,所以![]() .
.
因为四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
所以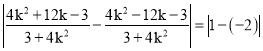 ,解得
,解得![]() 或
或![]() .
.
![]() 时,
时,![]() 与
与![]() 重合,不符合题意,舍去.
重合,不符合题意,舍去.
所以四边形![]() 为平行四边形时,
为平行四边形时,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




