题目内容
【题目】定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”;如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比,已知椭圆![]() .
.

(1)若椭圆![]() ,判断
,判断![]() 与
与![]() 相似?如果相似,求出
相似?如果相似,求出![]() 与
与![]() 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
(2)写出与椭圆![]() 相似且焦点在
相似且焦点在![]() 轴上,短半轴长为
轴上,短半轴长为![]() 的椭圆
的椭圆![]() 的标准方程;若在椭圆
的标准方程;若在椭圆![]() 上存在两点
上存在两点![]() 、
、![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围;
的取值范围;
(3)如图:直线![]() 与两个“相似椭圆”
与两个“相似椭圆”![]() 和
和![]() 分别交于点
分别交于点![]() 和点
和点![]() ,试在椭圆
,试在椭圆![]() 和椭圆
和椭圆![]() 上分别作出点
上分别作出点![]() 和点
和点![]() (非椭圆顶点),使
(非椭圆顶点),使![]() 和
和![]() 组成以
组成以![]() 为相似比的两个相似三角形,写出具体作法.(不必证明)
为相似比的两个相似三角形,写出具体作法.(不必证明)
【答案】(1)椭圆![]() 与
与![]() 相似,相似比为
相似,相似比为![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)由题意椭圆![]() 与
与![]() 相似,由椭圆
相似,由椭圆![]() 的特征三角形是腰长为4,底边长为
的特征三角形是腰长为4,底边长为![]() 的等腰三角形,能求出
的等腰三角形,能求出![]() 与
与![]() 的相似比.
的相似比.
(2)椭圆![]() 的方程为:
的方程为:![]() ,
,![]() ,设直线
,设直线![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中点为
中点为![]() ,
,![]() ,由
,由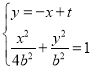 ,得
,得![]() ,由此利用韦达定理、根的判别式能求出实数
,由此利用韦达定理、根的判别式能求出实数![]() 的取值范围.
的取值范围.
(3)法1:过原点作直线![]() ,交椭圆
,交椭圆![]() 和椭圆
和椭圆![]() 于点
于点![]() 和点
和点![]() ,得到
,得到![]() 和
和![]() 即为所求相似三角形,且相似比为
即为所求相似三角形,且相似比为![]() .
.
法2:过点![]() 、点
、点![]() 分别做
分别做![]() 轴(或
轴(或![]() 轴)的垂线,交椭圆
轴)的垂线,交椭圆![]() 和椭圆
和椭圆![]() 点
点![]() 和点
和点![]() ,得到
,得到![]() 和
和![]() 即为所求相似三角形,且相似比为
即为所求相似三角形,且相似比为![]() .
.
解:(1)椭圆![]() 与
与![]() 相似.
相似.
因为![]() ,
,![]()
因为![]() ,
,![]()
因为椭圆![]() 的特征三角形是腰长为4,底边长为
的特征三角形是腰长为4,底边长为![]() 的等腰三角形,
的等腰三角形,
而椭圆![]() 的特征三角形是腰长为2,底边长为
的特征三角形是腰长为2,底边长为![]() 的等腰三角形,
的等腰三角形,
因此两个等腰三角形相似,且相似比为![]() .
.
(2)椭圆![]() 的方程为:
的方程为:![]() ,
,![]() ,
,
设直线![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中点为
中点为![]() ,
,![]() ,
,
则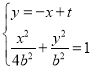 ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() 中点在直线
中点在直线![]() 上,
上,![]()
![]() ,
,![]() ,
,
即直线![]() 的方程为:
的方程为:![]() ,
,
由题意可知,直线![]() 与椭圆
与椭圆![]() 有两个不同的交点,
有两个不同的交点,
即方程![]() 有两个不同的实数解,
有两个不同的实数解,
![]()
![]() ,即
,即![]() .
.
(3)作法1:过原点作直线![]() ,交椭圆
,交椭圆![]() 和椭圆
和椭圆![]() 于点
于点![]() 和点
和点![]() ,
,
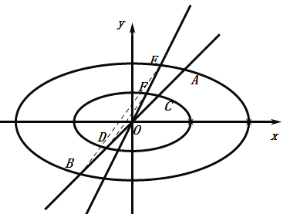
则![]() 和
和![]() 即为所求相似三角形,且相似比为
即为所求相似三角形,且相似比为![]() .
.
作法2:过点![]() 、点
、点![]() 分别做
分别做![]() 轴(或
轴(或![]() 轴)的垂线,交椭圆
轴)的垂线,交椭圆![]() 和椭圆
和椭圆![]() 点
点![]() 和点
和点![]() ,
,

则![]() 和
和![]() 即为所求相似三角形,且相似比为
即为所求相似三角形,且相似比为![]() .
.

 口算题天天练系列答案
口算题天天练系列答案【题目】某公司为了预测下月产品销售情况,找出了近7个月的产品销售量![]() (单位:万件)的统计表:
(单位:万件)的统计表:
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售量 |
|
|
|
|
|
|
|
但其中数据污损不清,经查证![]() ,
,![]() ,
, .
.
(1)请用相关系数说明销售量![]() 与月份代码
与月份代码![]() 有很强的线性相关关系;
有很强的线性相关关系;
(2)求![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)公司经营期间的广告宣传费![]() (单位:万元)(
(单位:万元)(![]() ),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
参考公式及数据:![]() ,相关系数
,相关系数 ,当
,当![]() 时认为两个变量有很强的线性相关关系,回归方程
时认为两个变量有很强的线性相关关系,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.


