题目内容
设函数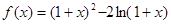
(1)若关于x的不等式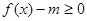 在
在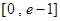 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设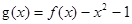 ,若关于x的方程
,若关于x的方程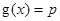 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.
(3)证明不等式: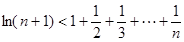
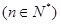
(1)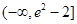 (2)p的最小值为0
(2)p的最小值为0
解析试题分析:
(1)存在性问题,只需要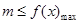 即可,再利用导数法求解f(x)的最大值(即求导,求单调性,求极值9与端点值比较得出最值).
即可,再利用导数法求解f(x)的最大值(即求导,求单调性,求极值9与端点值比较得出最值).
(2)p的最小值为函数g(x)的最小值,利用导数求函数的最小值即可(即求导,求单调性,求极值9与端点值比较得出最值).
(3)利用第二问结果可以得到与不等式有关的恒等式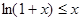 .令
.令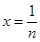 .把n=1,2,3,,得n个不等式左右相加,左边利用对数除法公式展开即可用裂项求和法得到不等式的左边,即证得原式
.把n=1,2,3,,得n个不等式左右相加,左边利用对数除法公式展开即可用裂项求和法得到不等式的左边,即证得原式
试题解析:
(1)依题意得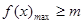
 ,而函数
,而函数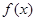 的定义域为
的定义域为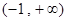
∴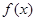 在
在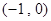 上为减函数,在
上为减函数,在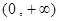 上为增函数,则
上为增函数,则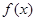 在
在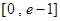 上为增函数
上为增函数
,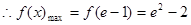 即实数m的取值范围为
即实数m的取值范围为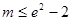 4分
4分
(2)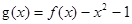
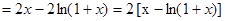 则
则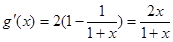
显然,函数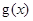 在
在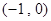 上为减函数,在
上为减函数,在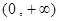 上为增函数,则函数
上为增函数,则函数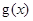 的最小值为
的最小值为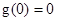
所以,要使方程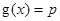 至少有一个解,则
至少有一个解,则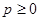 ,即p的最小值为0 8分
,即p的最小值为0 8分
(3)由(2)可知:  在
在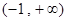 上恒成立
上恒成立
所以 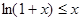 ,当且仅当x=0时等号成立
,当且仅当x=0时等号成立
令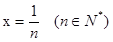 ,则
,则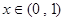 代入上面不等式得:
代入上面不等式得: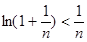
即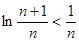 , 即
, 即 
所以,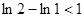 ,
,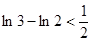 ,
,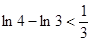 ,,
,,
将以上n个等式相加即可得到: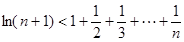 12分
12分
考点:导数 不等式 函数最值

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
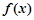 定义在区间
定义在区间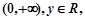 都有
都有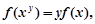 且
且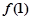 的值;
的值;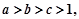 且
且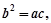 求证:
求证: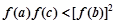 ;
;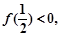 求证:
求证: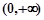 上是增函数.
上是增函数. 的定义域为
的定义域为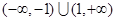 ,对定义域内的任意x,满足
,对定义域内的任意x,满足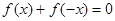 ,当
,当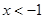 时,
时,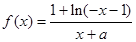 (a为常),且
(a为常),且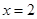 是函数
是函数 时,不等式
时,不等式 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;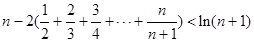
 两城相距
两城相距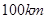 ,在两地之间距
,在两地之间距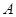 城
城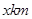 处
处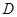 地建一核电站给
地建一核电站给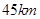 .已知供电费用(元)与供电距离(
.已知供电费用(元)与供电距离(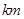 )的平方和供电量(亿度)之积成正比,比例系数
)的平方和供电量(亿度)之积成正比,比例系数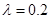 ,若
,若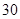 亿度/月,
亿度/月,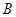 城为
城为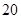 亿度/月.
亿度/月. 表示成
表示成 的函数,并求定义域;
的函数,并求定义域;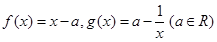 .
. 在
在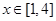 的单调性并用定义证明;
的单调性并用定义证明;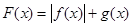 ,求
,求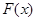 在区间
在区间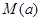 .
. .
. 有两个零点,求
有两个零点,求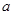 的取值范围;
的取值范围; 与
与 上各有一个零点,求
上各有一个零点,求 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.
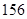 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?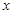 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为 (单位:厘米),已知当
(单位:厘米),已知当 时,
时,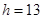 .试将
.试将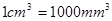 )
) .
.